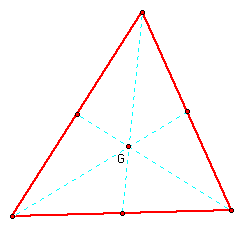
In this section, you will be required to construct the nine-point circle and locate the Euler Line involving this circle. We will put an inscribed triangle inside of a circle and then construct the medians, perpendicular bisectors and the altitudes of this triangle. This is done in the following picture.

We begin by constructing a nine-point circle.

First construct all the medians of a triangle, segments from a vertex to the midpoint of the opposite side and label it G.

Now construct the perpendicular bisectors of each side, this is the circumcenter, and label this point O.

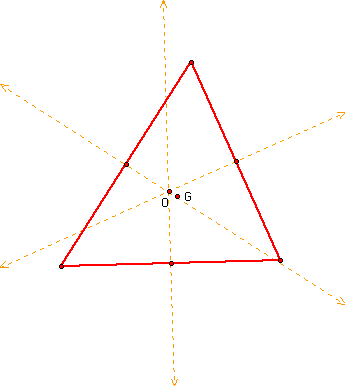
Now construct the orthocenter or the altitudes from each vertex and label this point H.

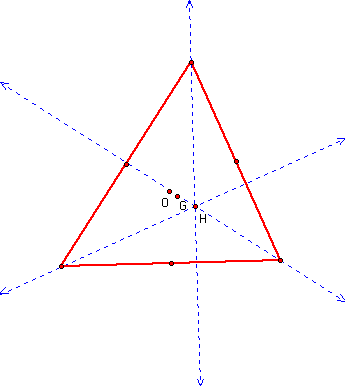
The nine - point circle travels through the bases of the three altitudes you have now created, the midpoints of the three sides, the midpoints between the orthocenter and each of the three vertices.

Use the GSP program to construct the nine-poiint circle on your own and look for relationships amongst the points and segments.

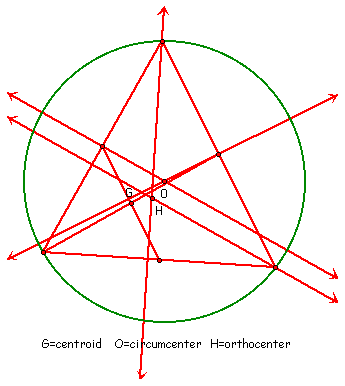
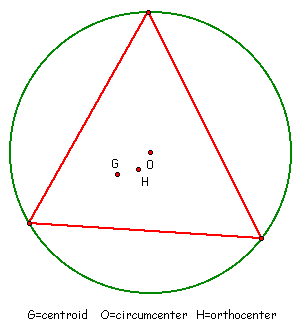
This first picture is with all of the construction marks included. As you can see, it is a bit clearer with the construction marks hidden.Line GO is the Euler Line. Give some special properties to this line by researching on the internet about it.