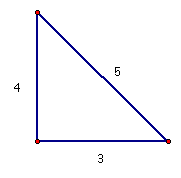
Pythagorean's theorem states, given a right triangle, the sum of the squares of the two legs equals the length of the hypotnuse squared. This theorem is used quite often inside a geometry classroom. I am wanting to provide students a couple different illustrations as to how this theorem works. I will give two different examples of proofs of this theorem and challenge students to underestand that solutions to a problem are not always unique. There are more ways than one to skin a cat.

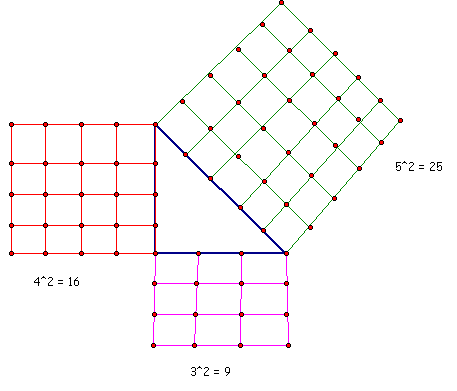
The pythagorean theorem can be displayed geometrically using actual squares. The formula a^2 + b^2 = c^2 may look a little different when displayed geometrically. This different representation may help a visual learner understand this theorem better. The geometrical representation would look like this.

I followed what the formula said and squared each side of the right triangle. If you count all the squares, you will see that the sum of the two legs squared equals the hypotenuse squared. This is a geometrical representation of the pythagorean theorem.

President James Garfield actually developed his own proof of the Pythagorean Theorem. It involved a trapezoid and its properties. Let's take a look at how President Garfield developed his proof by looking at a picture.

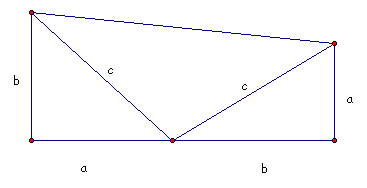
We know that the area of a trapezoid is the sum of its bases, times its height and divided by 2. In President Garfields problem, the bases are a and b, the height is a+b. By finding the areas of each of the right triangles in the trapezoid, we get ab/2 + ab/2 + c^2/2 = a^2/2 + 2ab/2 + b^2/2. With the ab terms cancelling out, we get a^2 + b^2 = c^2.

Research the internet to find other interesting representations of the pythagorean theorem.