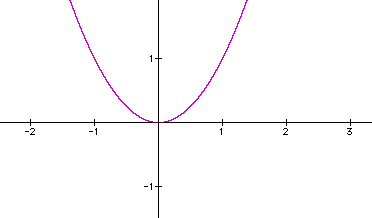
Quadratic Equation?

Let's try playing with the equation y=mx + b a little more. We have seen what happens when we change the b and the m, now let's change the x and see what happens to our line. Lets look at the graph of the equation y=x^2. (x squared)

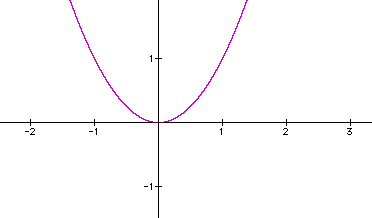
Our line is now curved. This is called a parabola. When our largest x term has an exponent of 2, this is the shape we get. Now let's see what happens when we write an equation with this term and alter its coefficient and the y-intercept.

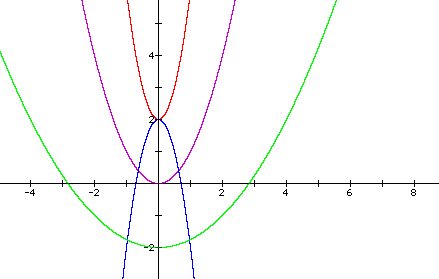
y=x^2

y=-4x^2+2

y=4x^2+2

y=x^2/4-2

By looking at the graph, you can tell that the y-intercept is still determined by the constant added or subtracted from the x term. The coefficient of the squared term determines the width of the parabola and the direction to which it opens. The closer to zero, the wider the parabola and a negative sign make it open downwards. The narrow parabolas have larger coefficients.