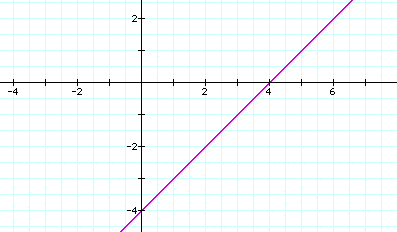
GRAPHIC SOLUTIONS TO AN EQUATION
In this section, we will take basic linear and quadratic equations, find their solutions, and compare these solutions to their graphs. Check to look for patterns between the solutions to the equation and the graphs.
First, let's look at the equation x + 3 = 7. By subtracting 3 from both sides and solving for x, we see that x = 4. The graph appears like this.
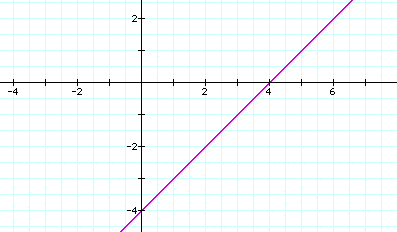
Notice the graph crosses the x-axis at 4, the same as the solution to the equation.
Now let us look at the quadratic equation x^2 + 4x = -3. To solve this equation, we subtract 3 from both sides, factor into two parentheses, then solve for x in each parentheses. We get (x+3) = 0 and (x+1) = 0. Our solutions are x = -3 and x = -1. Two possible solutions for this quadratic equation. Let's look at the graph.
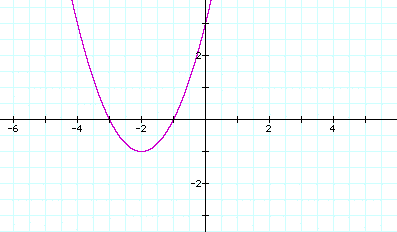
Our graph is a parabola that opens upward with a horizontal shift to the left of 2 units. It crosses the x-axis at -3 and -1. These are also the solutions to this equation.
Further investigations will reveal this is
true for all equations, regardless of the degree of the polynomial.
The solutions to the equation are the locations of the x-intercepts
if graphically displayed. These are solutions to x when y is 0.
RETURN