SOLVING A SYSTEM OF EQUATIONS

We now know how to find a solution to an equation through graphical interpretation. What about when we have a system of equations to solve, or more than one equation related to given variables? Let us look at a system of equations, solve it, and look at the graph of this system.

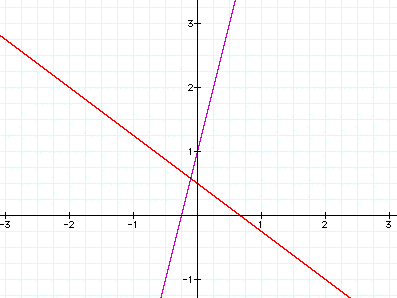
Let's look at the system

y = 4x + 1

3x +4y = 2

Multiply the bottom equation by -4 so that the y's cancel. Solving for x gives us x=-2/19. By substituting back into the equation, we learn that y = 11/19. These are not nice and neat numbers, but they are the solution to this equation. Let's look at the graph of this system, both equations on the same coordinate plane.

Look at the coordinates of the intersection point of these two lines. This coordinate is the same as our solution from above.

Graphically, the solution to a system of equations is a bit different than the solutions to a single equation. It is not where the lines cross the x-axis, but where the lines cross each other.