We will be investigating Sylvester's Triangle Problem: The resultant of the vectors represented by the 3 radii from the center of a triangle's circumcenter is the segment extending from the circumcenter to the orthocenter.

Each type of triangle including the acute, right, and obtuse is to be investigated. Each investigation is done using Geometer's Sketchpad.

Acute Triangle:

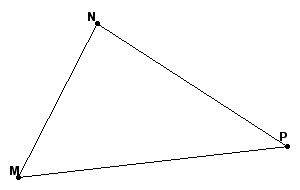
Begin with the acute triangle MNP.

First, find the circumcenter of the acute triangle. The circumcenter (C) is the point in the plane equidistant from the three vertices of the triangle. The first step to finding the circumcenter is to construct the midpoints of each side of the triangle.

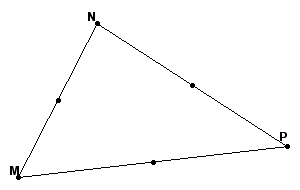
The next step is to construct the perpendicular bisector for each side of the triangle, since a point equidistant from two points lies on the perpendicular bisector of the segment determined by the two points.

The perpendicular bisector of segment MN is the red line.

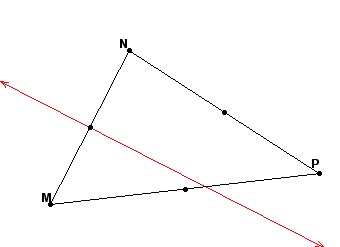
Next, construct the perpendicular bisector of segment NP, which is the blue line.

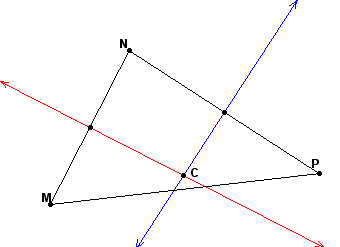
Finally, construct the perpendicular bisector of segment MP, which is the green line. The circumcenter C is the intersection of the three perpendicular bisectors.

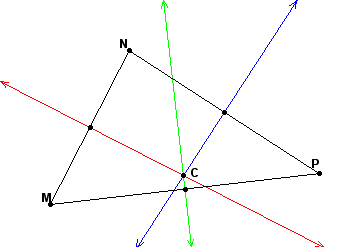
Construct the vectors CN, CM, and CP.

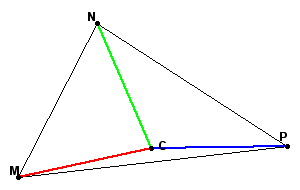
Starting with vector CN, add to it vector CP. To do this, construct a circle of radius CP with center C.

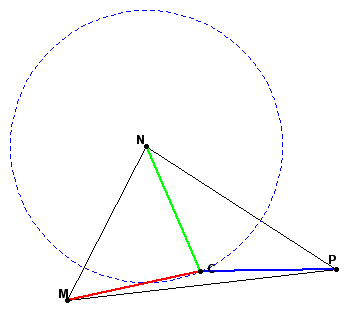
Then construct a line parallel to segment CP. The point where the parallel line intersects the circle is the endpoint of the new vector.

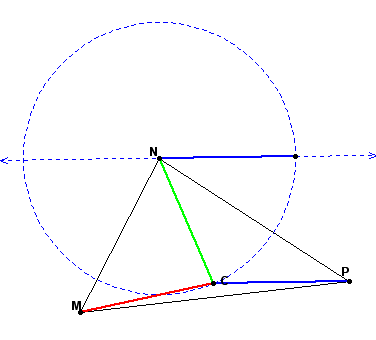
Add to the resultant vector CM, by constructing a circle with radius equal to CM at the endpoint of the resultant vector of CN and CP.

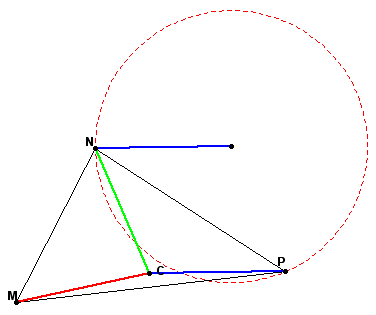
Construct a line parallel to CM and the point where the parallel line intersects the circle is the endpoint of the new vector.

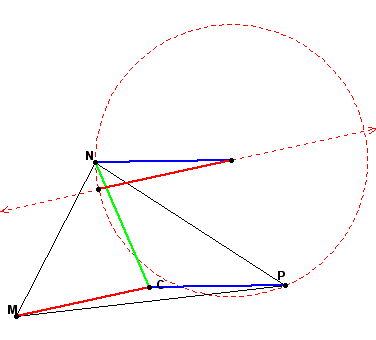
Finally, construct the segment CH, which is the resultant vector of CN, CP, and CM.

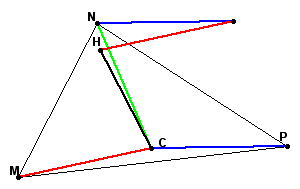
The new point H appears to lie of each of the altitudes of the triangle. To determine if this is accurate, construct the altitudes of triangle MNP.

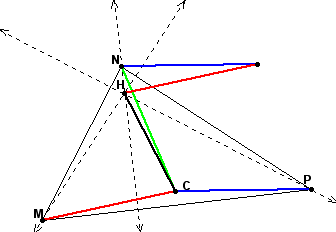
The point H is the intersection of each of the altitudes of triangle MNP, and therefore is the orthocenter of the triangle. So, we have shown using constructions that the resultant of the vectors represented by the 3 radii from the center of a triangle's circumcenter is the segment extending from the circumcenter to the orthocenter for an acute triangle.

Right Triangle:

Consider the case of the right triangle. Consider right triangle MNP.

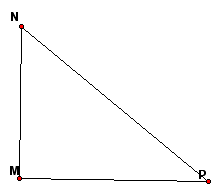
Find the circumcenter of the triangle by constructing the perpendicular bisectors of each side of the triangle.

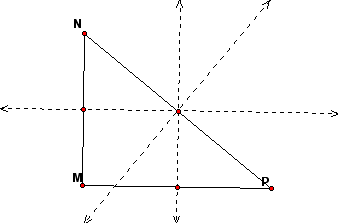
The intersection of these perpendicular bisectors is the circumcenter C. Then construct the vectors CM, CN, and CP.

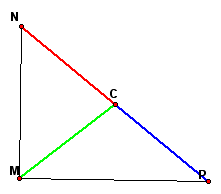
Starting with vector CN, add to it vector CM. To do this, construct a circle of radius CM with center C. Then construct a line parallel to segment CM.

The endpoint of the resulting vector is the point of intersection of the circle and the line parallel to segment CM.

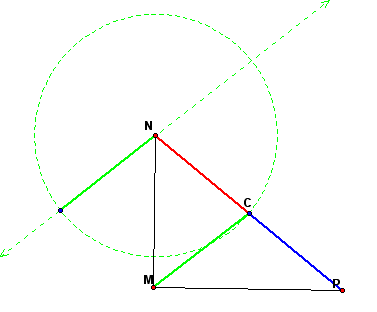
Next, add vector CP. To do this, construct a circle of radius CP with the center at the new endpoint of the resultant vector of CN and CM.

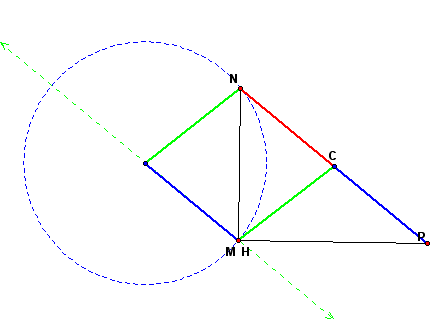
Finally, construct the segment CH, which is the resultant vector of CN, CP, and CM. The new point H coincides with point M of the original right triangle. To determine if point H is the orthocenter of the triangle, construct the altitudes of triangle MNP.

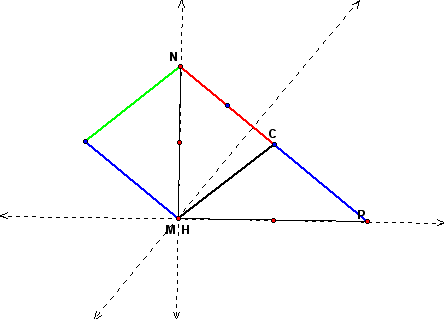
After constructing the altitudes of the right triangle, point H does actually coincide with point M and is the orthocenter of the right triangle. So, we have shown through constructions that the resultant of the vectors represented by the 3 radii from the center of a triangle's circumcenter is the segment extending from the circumcenter to the orthocenter for a right triangle.

Obtuse Triangle:

Consider the case of the obtuse triangle. Construct obtuse triangle MNP.

Find the circumcenter of the triangle by constructing the perpendicular bisectors of each side of the triangle.

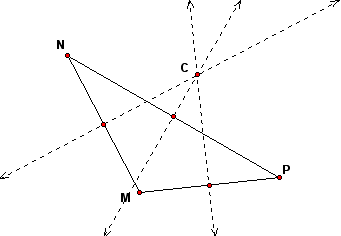
The intersection of these perpendicular bisectors is the circumcenter C. Then construct the vectors CM, CN, and CP.

Starting with vector CN, add to it vector CM. To do this, construct a circle of radius CM with center C. Then construct a line parallel to segment CM.

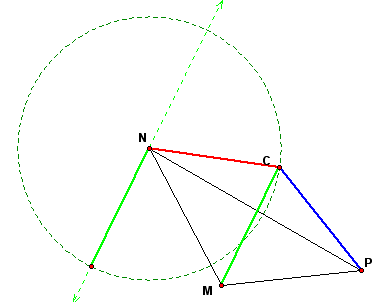
The endpoint of the resulting vector is the point of intersection of the circle and the line parallel to segment CM.

Next, add vector CP. To do this, construct a circle of radius CP with the center at the new endpoint of the resultant vector of CN and CM.

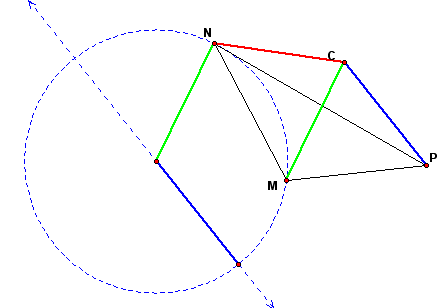
Finally, construct the segment CH, which is the resultant vector of CN, CP, and CM.

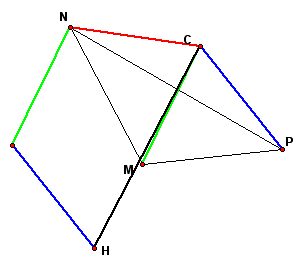
To determine if point H is the orthocenter of the triangle, construct the altitudes of triangle MNP.

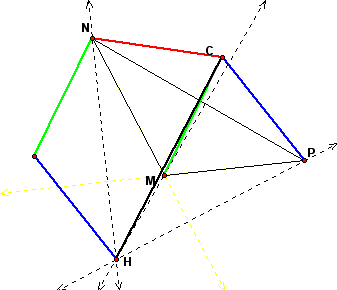
After constructing the altitudes of the obtuse triangle, point H is the orthocenter of the obtuse triangle. So, we have shown through constructions that the resultant of the vectors represented by the 3 radii from the center of a triangle's circumcenter is the segment extending from the circumcenter to the orthocenter for an obtuse triangle.

So we have considered the cases of the acute, right, and obtuse triangles for Sylvester's Triangle Problem. The resultant of the vectors represented by the three radii from the center of a triangle's circumcircle to its vertices is the segment extending from the circumcenter to the orthocenter.

Return to Chris Reid's home page