Fagnano's Problem:

To inscribe in a given acute-angle triangle the triangle of a minimum perimeter. I.F. Fagnano (1775)

First, construct a triangle with three acute angles, triangle ABC.

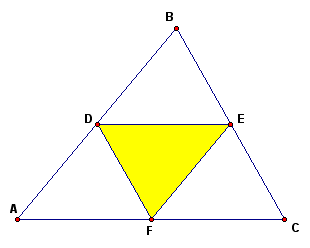
Find the midpoints of each of the sides of the triangle, and make a triangle using the three midpoints as the vertices, triangle DEF.

The measures of each of the sides of the inscribed triangle DEF are

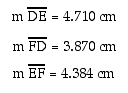
The perimeter of trianlge DEF is

This perimeter gives a perimeter with which to compare perimeters of other inscribed triangles.

Trisect each side of triangle ABC, and construct another inscribed triangle.

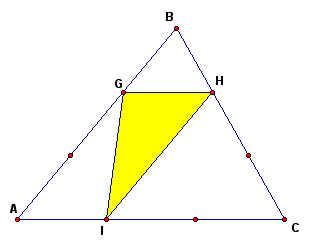
By constructing triangle GHI, the measures of each of the sides are

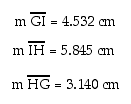
The perimeter of triangle GHI is

This is larger than the triangle constructed using the midpoints.

Next, find the angle bisectors of each angle of triangle ABC.

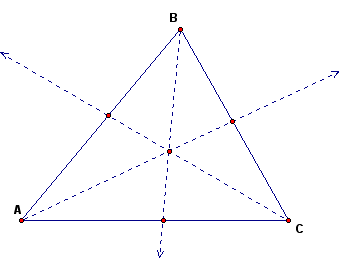
Construct the triangle formed using these new points, triangle JKL.

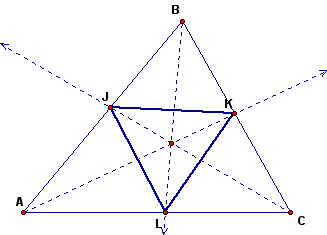
The length of each side of triangle JKL is

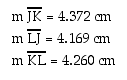
The perimeter of triangle JKL is

This is smaller than the perimeter of triangle DEF, made from the midpoints of the sides of triangle ABC.

Another possible inscribed triangle is formed using the altitudes of triangle ABC.

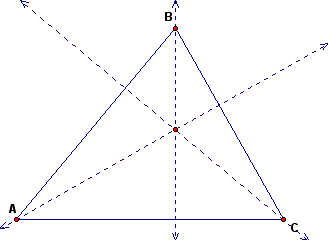
Construct the inscribed triangle from the points of intersection with each side of triangle ABC.

The new triangle is triangle PQR.

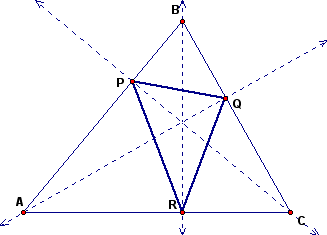
The lengths of each side of triangle PQR are

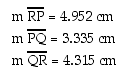
The perimeter of triangle PQR is

This perimeter is smaller than the perimeter of the triangle formed using the angle bisectors. This triangle is called the orthic triangle. The orthic triangle is actually the inscribed triangle of any acute-angle triangle with the least perimeter.

Return to Chris Reid's home Page