Objective:

Find 2 linear functions f(x) and g(x) such that their product

is tangent to each f(x) and g(x) at two distinct points. The objective is illustrated below.

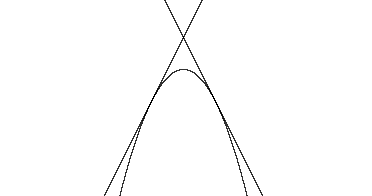
Begin by noticing that the slopes of the linear functions must be of opposite signs - one negative and one positive.

Select possible linear functions

Then graph.

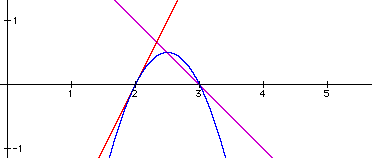
By graphing f(x), g(x), and the product function h(x), the graph yields one tangent point to g(x) and two points of intersection with f(x).

Change f(x) and g(x),

The new h(x) function is

 

The new graph is

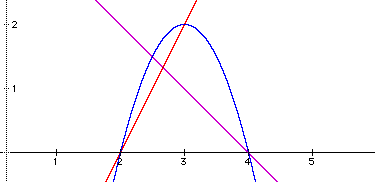
This graph yields two points of intersection with f(x) and two points of intersection with g(x).

Looking again at the objective illustration, notice the slopes of the lines appear to be opposites.

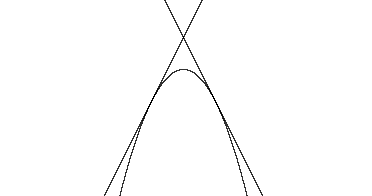
Change f(x) and g(x) again.

Then graph.

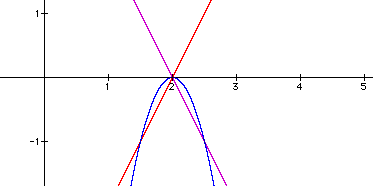
This yields three points of intersection.

Make adjustments to f(x) and g(x) by changing the y-intercepts.

Try

Then graph.

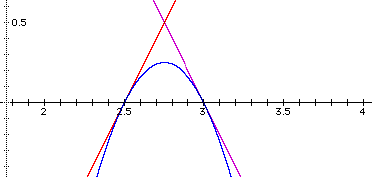
The function h(x) appears to be tangent to f(x) and g(x).

After solving equations f(x) and h(x) simultaneously, the point of intersection is (3,0). After solving equations g(x) and h(x) simultaneously, the point of intersection is (2.5,0). Since each linear equation intersects h(x) at only one point, h(x) is tangent to f(x) and g(x) at two distinct points meeting the objective.

Return to Class Page