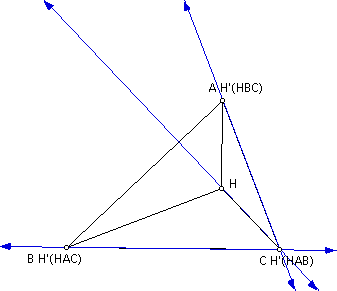
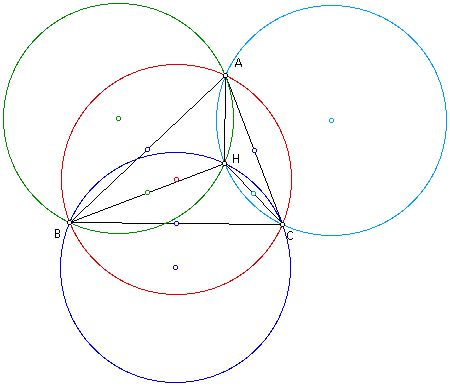
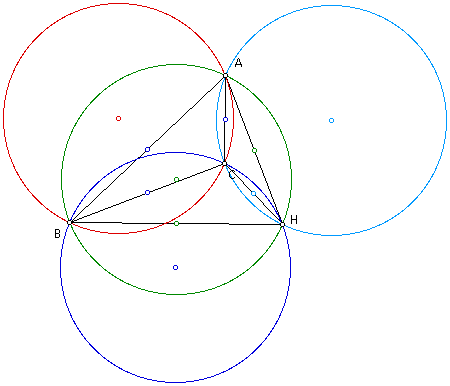
Construct any triangle ABC.

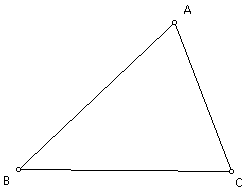
Construct the orthocenter H of triangle ABC.

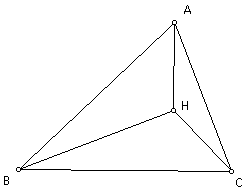
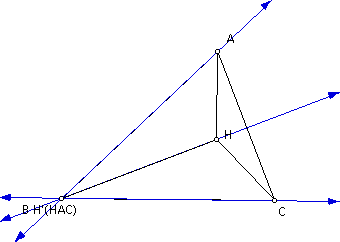
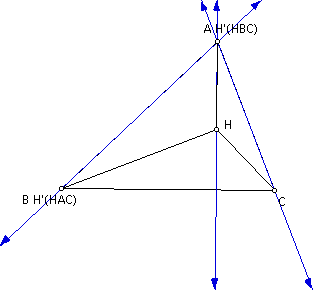
Construct the orhtocenter H' (HAC) of triangle HAC.

Construct the orthocenter H' (HBC) of triangle HBC.

Construct the orhtocenter H' (HAB) of triangle HAB.

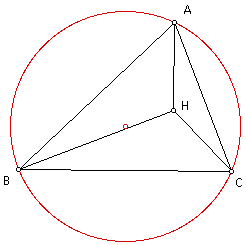
Construct the circumcircle of triangle ABC.

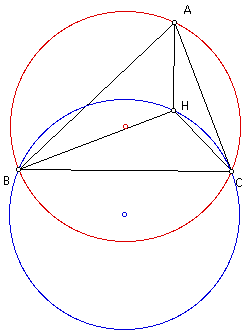
Construct the circumcircle of triangle HBC.

Construct the circumcircle of triangle HAB.

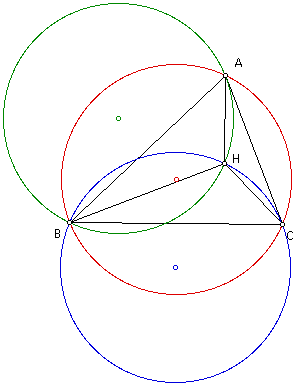
Construct the circumcircle of triangle HAC.

Problem 7:

Using theorems of chords and radii, congruent triangles, and theorems of parallelograms, we can say that AQBP is a rhombus. Also, using similar arguments, BRCP is a rhombus congruent to AQBP. And also that SAPC is also a rhombus and congruent to AQBP. Therefore, since all sides are congruent and all sides are radii of the circumcircles, then the radii are congruent and the circumcircles are congruent.

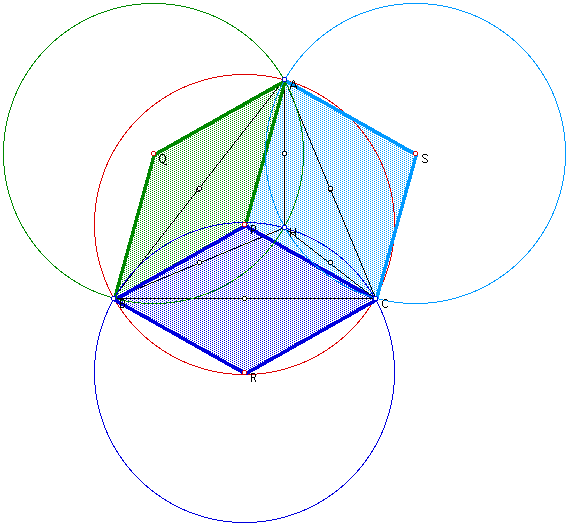
Conjecture: The circumcircles are congruent.

For the figure constructed, what would happen if any vertex of the triangle ABC was to move to where the orthocenter H is located?

1. Click here to see what would happen if A was to move to H.

2. Click here to see what would happen if B was to move to H.

3. Click here to see what would happen if C was to move to H.

4. Click here to see what would happen if A moves to H, B moves to H, and then C moves to H.

If A was to move to H, then H would move to where A had been before the move. The circumcircles are still in the locations of the four circumcircles before the move.

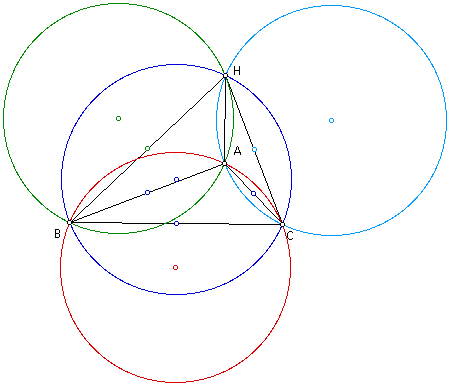
If B was to move to H, then H would move to where B had been before the move. The circumcircles are still in the locations of the four circumcircles before the move.

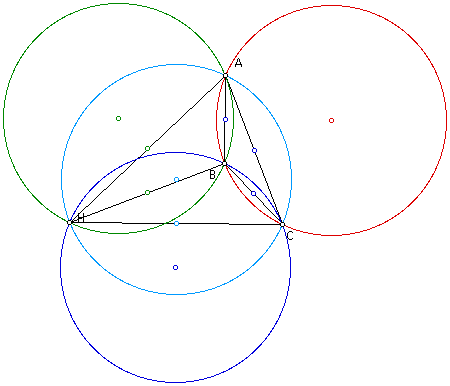
If C was to move to H, then H would move to where C had been before the move. The circumcircles are still in the locations of the four circumcircles before the move.

If A moves to H then B moves to H and then C moves to H, the figure looks the same. The circumcircles are still in the locations of the four circumcircles before the move.

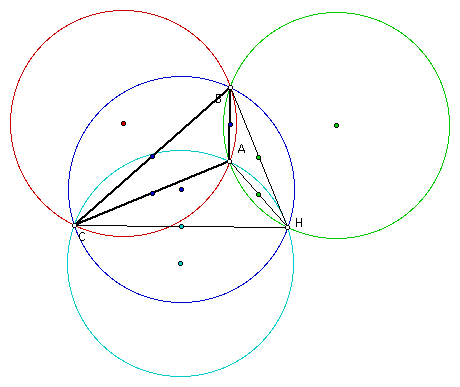
Conjecture:

The orthocenters and circumcircles remain the same regardless of the movement of any vertex of the triangle ABC to the location of the orthocenter H.