Let triangle ABC be any triangle.

Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary) locate points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

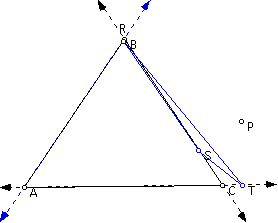
Click here for a GSP script for a pedal triangle construction.

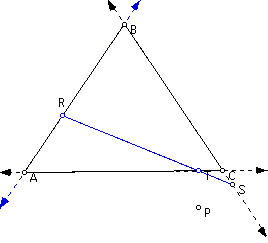
It appear that for some positions of point P in the plane, the pedal triangle does not exist as a triangle. There are some instances where R, S, and T are collinear. This line is called the Simson Line.

What happens when the pedal triangle is the centroid of triangle ABC?

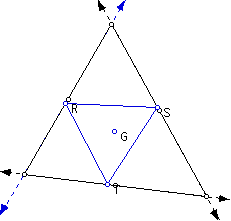
The triangle is in the interior of triangle ABC as long as R, S, and T lie between A, B, and C.

When R, S, or T coincides with a vertex A, B, or C, the pedal triangle becomes a right triangle.

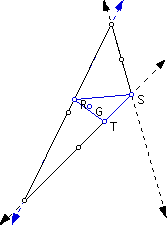
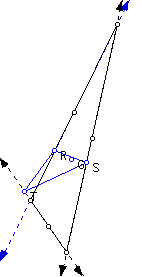
When R, S, or T move outside of the vertices A, B, or C the pedal triangle then moves outside the original triangle at that vertex.

Return to Class Page