I will do a very basic exploration of a parabola and how changing one value in the equation while keeping the others constant will change the graph.  The values that will be used are a, b, and c.  Which values will shift the graph to the left or right?  What makes the graph move up and down the y-axis?  What makes the parabola flatten out or become skinnier?

Our equation is  y= ax2 + bx + c.

I will change the c value first while keeping a and b constant at one.

y= x² + x + 0.5
y= x² + x + 1
y= x² + x +1.5
y = x² + x + 2



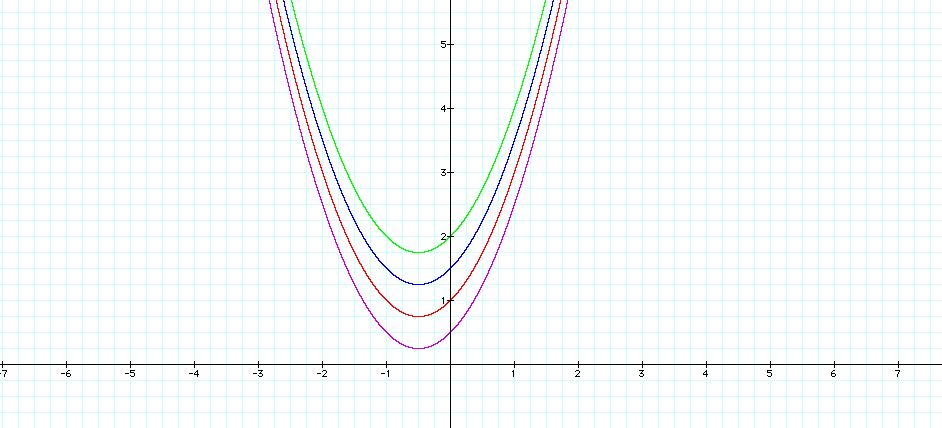
The changing of the c value shifts the parabola up and down the y-axis while not changing the shape nor moving is from left to right.  The y-intercept can be calculated by putting an x value of 0 in and solving the equation for y.  So one can see both on the graph and algebraically that the c value is the y intercept.

Next the b value will be varied while the a and c values will be kept constant at one.

y= x² + 0.5x + 1
y= x² + x + 1
y= x² + 1.5x +1
y = x² + 2x + 1

We should speculate ahead of time how changing the b value will affect the graph.  Will it again shift the parabola up and down the y-axis?  Will it change the shape at all?  Or will it move the graph from left to right or right to left?  Now we will see.

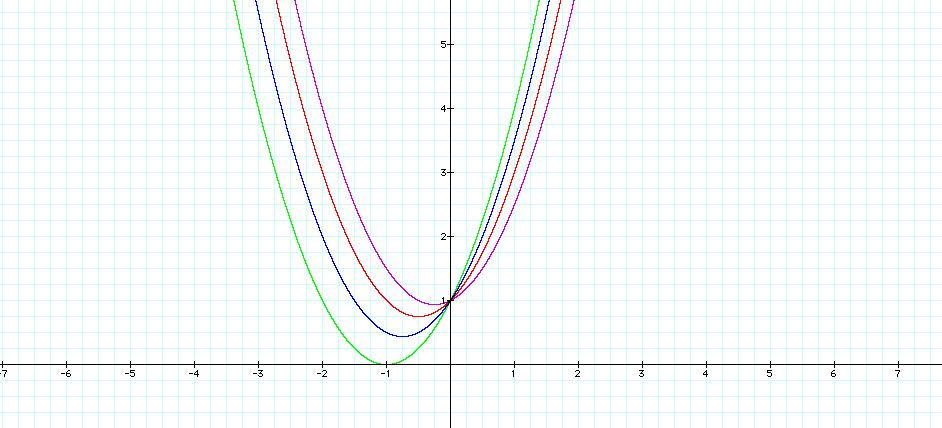
At first glance it looks as if the graphs shifted up and to the right.  But on closer inspection that is not true.  They simply moved to the right.  The y-intercept never changed.  It's almost as if there is a loop on the point (0,1) and the graph has to slide through that loop to move.

Now we have seen the graph move up and down the y-axis and shift from left to right.  Do you think that changing the a value will repeat either of those or do something different?

y= 0.5x² + x + 1
y= x² + x + 1
y= 1.5x² + x +1
y = 2x² + x + 1



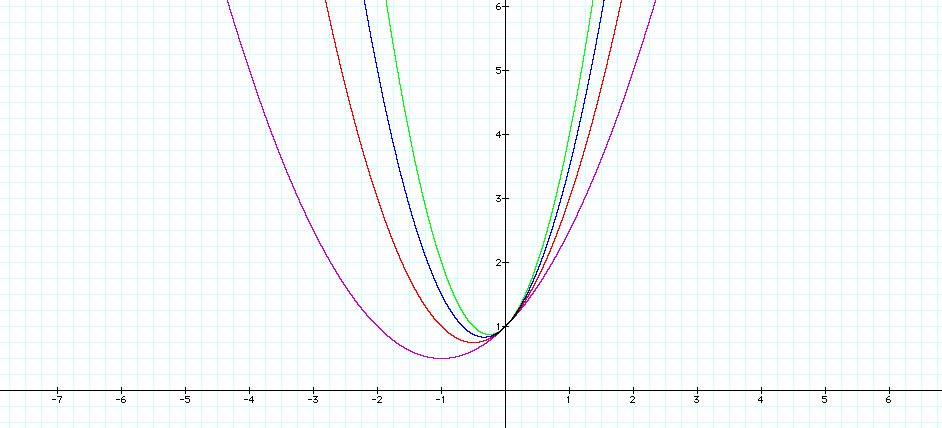
The slope has stayed at (0,1).  It also looks as if the location of the minimum of each graph is the same as when the value b was at one in the first example.  But the shape of the graphs has changed.  The smaller the a value the "fatter" the parabola is.

I really enjoy working with this software.  It will be invaluable for the visual student.  Color coding the lines enables the learner to better see how the graph has changed as the values change.