Exploring Pedal Triangles
Sharon Sewell
Fall 2001
This will be an exploration of pedal triangles. I will create several different triangles and the respective pedal triangles using the incenter, the centroid, the orthocenter and the circumcenter as the point P for creating the pedal triangle. Then I will look at the triangle created. Is it special in anyway? If so, why do I think it is unique?
A pedal triangle is formed when some point is chosen in a plane, from that point lines are drawn perpendicular to the sides of a given triangle in the plane. The points of intersection of those lines form the vertices of the pedal triangle.
Example:
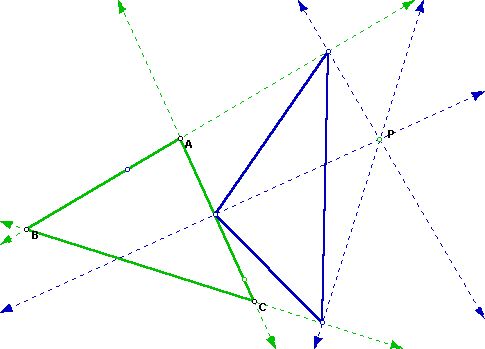
Notice that the triangle sides had to be extended beyond the vertices of the triangles. These extensions are shown by the dotted lines in green. The blue dotted lines show the path of the perpendicular line going from the random point P to the side of the triangle. When the points of intersections connected then the pedal triangle is formed.
Let’s play with this type of construction some. What
would happen if P were the incenter of the triangle?
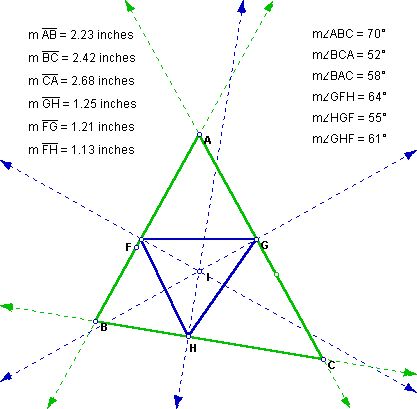
When the main triangle is an equilateral triangle so is the pedal triangle. When the main triangle is an isosceles triangle so seems to be the pedal. Click here to manipulate the triangle yourself (pedal2.gsp).
We will now use the centroid of a triangle as the
point P.
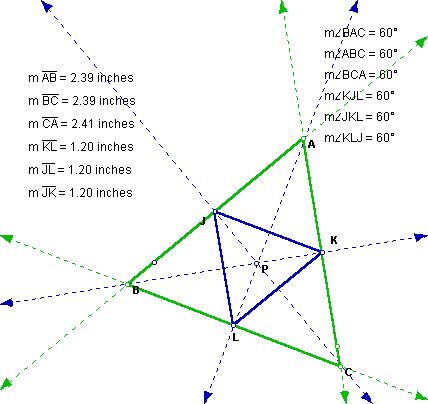
When the main triangle is an equilateral triangle so is the pedal triangle. When the main triangle is an isosceles triangle so is the pedal. And finally when the main triangle is a right triangle the pedal triangle is also an isosceles triangle. To see this click here and move the triangles around to form each. (pedal3.gsp).
What do you think will happen if we use the orthocenter as point P? Remember that the orthocenter is when a perpendicular line is drawn from one of the vertices to the opposite side. This is done for all of the vertices in the triangle and the point of intersection is the orthocenter. Now we will look at the pedal triangle formed by using the orthocenter.
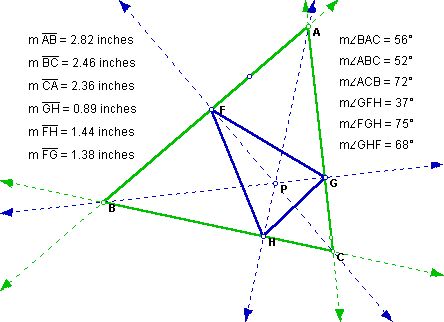
When the orthocenter is used as P, and an equilateral triangle is the main triangle then the pedal triangle formed is also equilateral. By the same token, when the main triangle is an isosceles triangle then the pedal triangle formed is also isosceles. But the most interesting discovery I made was when the main triangle is a right triangle the pedal triangle becomes a straight line. Explore this yourself by clicking here and moving the triangles around. (pedal4.gsp)
And now the circumcenter:
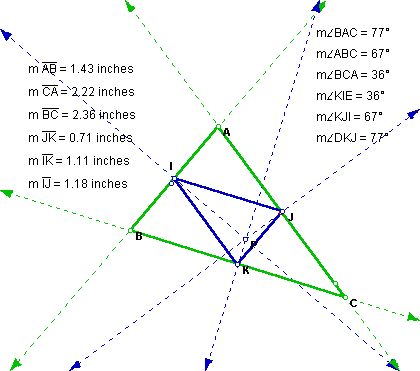
Using the circumcenter as the point P in forming the pedal triangle creates a triangle that is equal to the main triangle. This means that the measures of the angles in the main triangle equal the measure of the angles in the pedal triangle. Consequently, when the main triangle is a right triangle so is the pedal triangle. And when the main triangle is an isosceles triangle so is the pedal triangle. And finally when the main triangle is an equilateral triangle so is the pedal triangle. Click here to explore this. (pedal5.gsp).
There are so many ways look at the pedal triangle these were just a few.