In this write-up, I examine the graph of the following parametric equation:
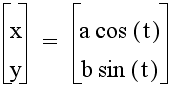
for different values of the coefficients a and b. The graphs will be explored for values of t greater than or equal to zero and less than or equal to 2 pi.
The graph of the parametric equation that results for a = 1 and b = 1:
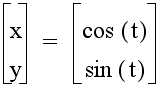
becomes the graph of the unit circle shown below:

When the value of b equals zero, the parametric equation becomes
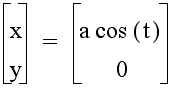
for which the graph is the line segment with endpoints (-a, 0) and (a, 0). Similarly, when a equals zero, the equation is
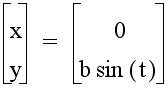
for which the graph is the line segment with endpoints (0, -b) and (0, b). The graph when a equals zero and b equals zero is just the origin (0, 0).
If we leave the value of b equal to one and vary the coefficient a, the equation becomes
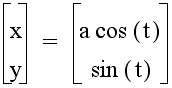
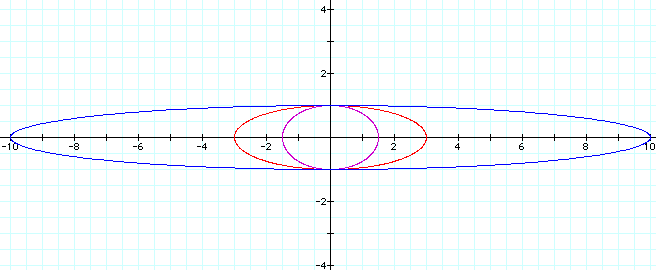
For values of a > 1, the graph is an ellipse with a horizontal major axis of length 2*a. The figure below shows the graphs for a = 1.5 (purple graph), a = 3 (red graph), and a = 10 (blue graph).
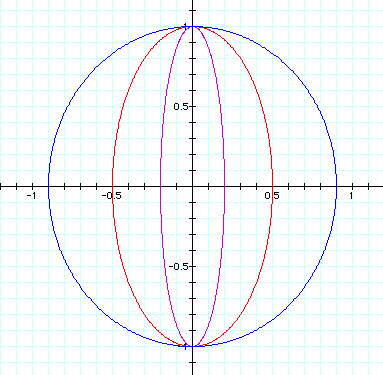
The graph for a = 1 is a circle as shown previously. When 0 < a < 1, the graph is an ellipse with a vertical major axis of length 2. The figure below shows the graphs for a = .2 (purple graph), a = .5 (red graph), and a = .9 (blue graph).
The graph when a equals zero is the line segment with endpoints (0, -1) and (0, 1). The graphs for values of a < 0 are identical to the graphs of the absolute value of a.
If we leave the value of a equal to one and vary the coefficient b, the equation becomes
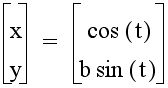
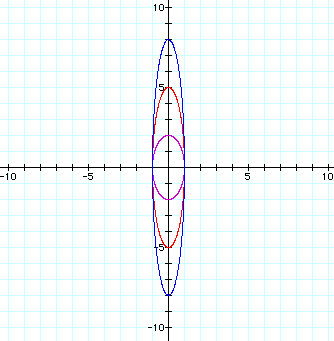
For values of b > 1, the graph becomes an ellipse with a vertical major axis of length 2*b. The figure below shows graphs for b = 2 (purple graph), b = 5 (red graph), and b = 8 (blue graph).
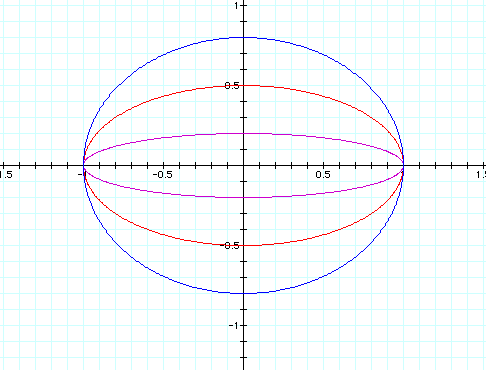
The graph for b = 1 is a circle as shown previously. When 0 < b < 1, the graph is an ellipse with a horizontal major axis of length 2. The figure below shows graphs for b = .2 (purple graph), b = .5 (red graph), and b = .8 (blue graph).
The graph when b equals zero is the line segment with endpoints (-1, 0) and (1, 0). The graphs for values of b < 0 are identical to the graphs of the absolute value of b.
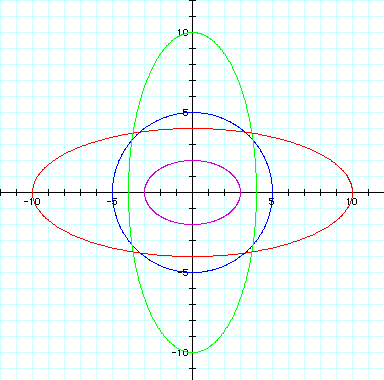
When both a and b are varied, the graph is an ellipse with the length of the horizontal axis equal to 2*a and the length of the vertical axis equal to 2*b. For values of a > b, the horizontal axis is the major axis. For values of a < b, the vertical axis is the major axis. For values of a = b, the ellipse is a circle with radius a = b.
The figure below shows graphs for a = 3, b = 2 (purple graph); a = 10, b = 4 (red graph); and a = 5, b = 5 (blue graph); and a = 4, b = 10 (green graph).