In this write-up, I examine the graphs of the equation
for different values of the coefficients a, b, and k. We will explore what happens when a and b are equal and k is varied as an integer. The variations for the graph when a is equal to zero will be investigated. The change in the graph when the cosine function is replaced with the sine function will also be observed.
When a, b, and k are equal to one, the following equation results:
This equation results in the figure of a single petaled rose as shown below
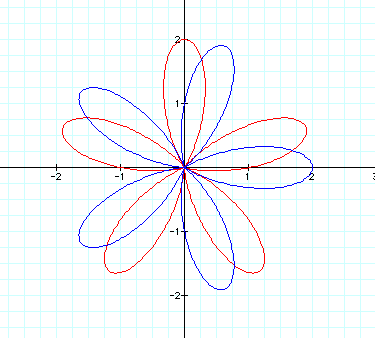
When a and b equal one and k is varied as an integer, the graph becomes that of a rose with k petals. The figure below shows the graphs for k = 2 (red graph) and k = 7 (blue graph).
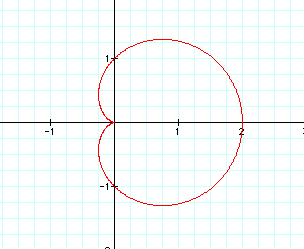
If a and k equal one and b is varied as an integer, the graph is a single petal with a loop within the petal. As b increases, the size of the loop increases, and the size of the inner loop approaches the size of the surrounding petal. The figure below shows the graphs for b = 2 (red graph) and b = 10 (blue graph).
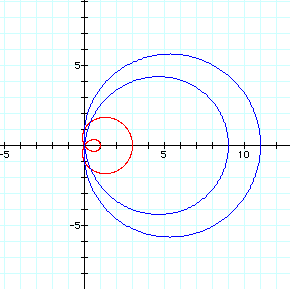
If b and k equal one and a is varied as an integer, the graph is a single petal that quickly approaches a circular figure. As a increases, the size of the single loop increases, and the shape of the graph approaches a circle. The figure below shows the graphs for a = 2 (red graph) and a = 5 (blue graph).
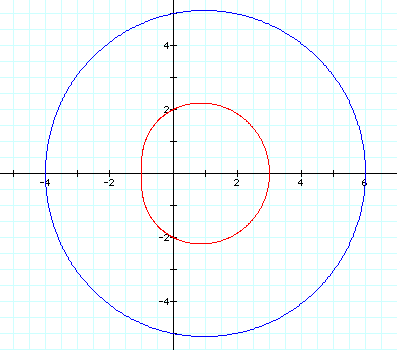
We have seen already that when a and b equal one, the value of k represents the number of petals in the rose. If a and b remain equal but are different values, then the value of k determines the number of petals in the rose and the value of a and b determines the size of the petals. For the equation
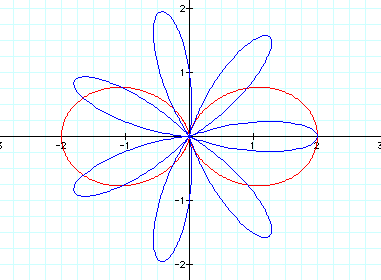
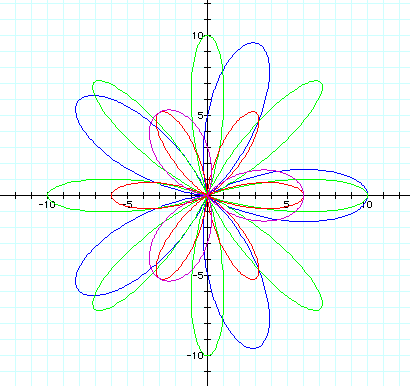
with a = b, the graph is a rose with k petals that are each 2*a in length. The figure below shows the graphs for a = b = k = 3 (purple graph), a = b = 3 and k = 6 (red graph), a = b = k = 5 (blue graph), and a = b = 5 and k = 8 (green graph).
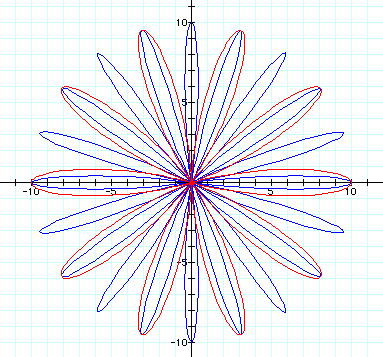
The pattern of a rose with k petals continues even for larger values of k, as shown in the figure below with a = b = 5; k = 10 (red graph) and k = 20 (blue graph).
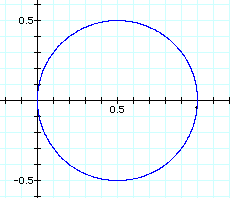
If the coefficient a is set equal to zero, then the following equation results:
The graph when b = k = 1 appears to be a circle with radius of .5 as shown below:
If b increases while k is held constant, then the size of the loop increases by a factor of b. If b remains constant and k is varied, then the graphs become roses with the number of petals being a function of k. When k is an odd integer, then number of petals is equal to k and when k is an even integer, the number of petals is equal to 2*k. The figure below shows the graph for k = 3 (blue graph) and k = 6 (red graph).
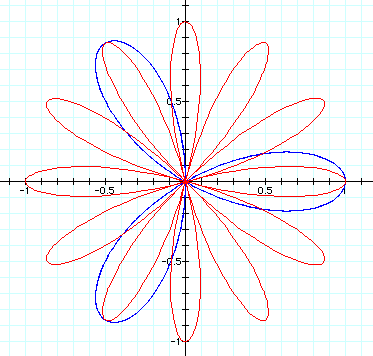
When k is not an integer, then the graph results in fractional petals with the number of petals being 2*k. The figure below shows the graph for k = 2.5 (blue graph) and k = 3.3 (red graph).
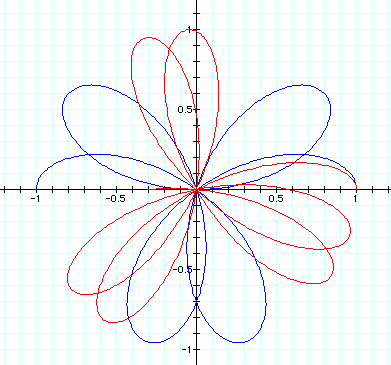
The result of non-integer values of k demonstrates that the fact that the number of petals for the graph is always 2*k. However, when k is an odd integer, the values of the cosine of k*theta for theta from 0 to pi is equal to the values of the cosine of k*theta for theta from pi to 2 pi. So half of the petals overlap themselves when k is an odd integer, showing only k petals in the graph.
If the cosine function is replaced by the sine function in the original equation, the following equation results:
The figure below shows the graph of this equation (red graph) and the original equation (blue graph) for a = b = k = 1.
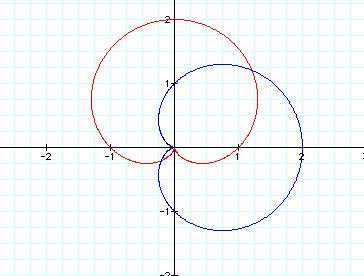
Further exploration with various value of k when a = b = 1 remains constant shows that the graphs remain similar, only varying by rotation around the origin. The rotation of the graph of the sine function from the cosine function is a function of the coefficient k. For a given value of k, the graph of the sin equation will be the graph of the original cosine equation rotated counterclockwise by a value of pi/(2*k) radians. As the value of k increases, the graph of the sine equation approaches the graph of the original equation because the degree of rotation gets smaller. The figure below shows the graph of the sine equation for k = 2 (red graph) and the original equation for k = 2 (blue graph). Note that the amount of rotation is pi/4.
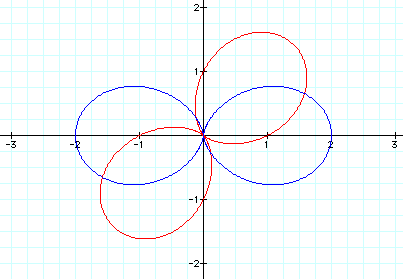
To see the decreasing degree of rotation, observe the graph below of the sine equation for k = 5 (red graph) and the graph of the original equation for k = 5 (blue graph).