

It has now become a rather standard exercise, with availble
technology, to construct graphs to consider the equation
and to overlay several graphs of
for different values of a, b, or c as the other two are held
constant. From these graphs discussion of the patterns for the
roots of
can be followed. For example, if we set
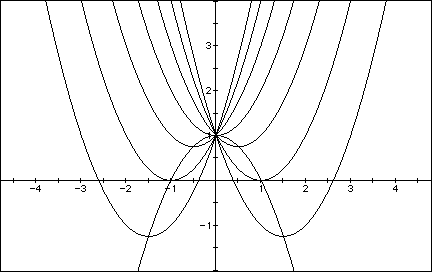
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the
following picture is obtained.

Consider that the solution set for the equation
for these same values of b can be found by determining where the graph of
crosses the x-axis for the given value of b.
We can discuss the characterisitcs of the solution set by observing
the "movement" of a parabola as b is changed. The parabola
always passes through the same point on the y-axis ( the point
(0,1) with this equation). For values of b < -2, the parabola
will intersect the x-axis in two points with positive x values
(i.e. the original equation will have two real roots, both positive).
For b = -2, the parabola is tangent to the x-axis and so the original
equation has one real positive root at the point of tangency.
For -2 < b < 2, the parabola does not intersect the x-axis,
and therefore the original equation has no real roots. Similarly
for b = 2 the parabola is tangent to the x-axis (one real negative
root) and for b > 2, the parabola intersets the x-axis twice
at the values for the two negative real roots for each b.
Now consider the locus of the vertices of the set of parabolas
graphed from
Consider that the vertex is the point (h, k) in the general
form of the parabola ![]()
and that for the given equation a = 1, so we have the equation
![]()
which becomes ![]()
Considering that k represents y, h represents x, we can substitute the point (0, 1), which is always on the graph of the original parabola, regardless of the value of b. This gives us the equation
and substituing y for k and x for h and then solving for y gives us the equation for the locus of the vertices of the parabolas graphed from the original equation.
Now we will consider the following equation
When this equation is graphed in the xa plane, we have the following graph.
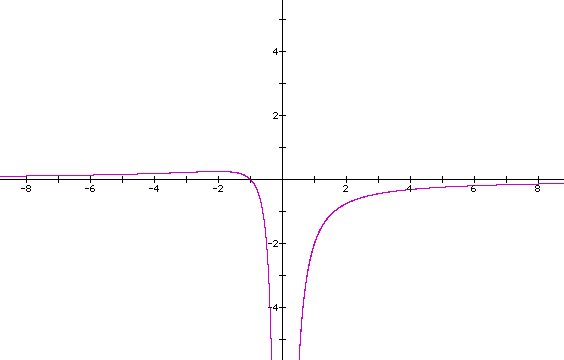
If we consider the graph of a specific value of a, and overlay this onto the original graph this adds a line parallel to the x-axis. If this line intersects the curve in the xa plane, then the points of intersection correspond to the roots of the original equation for the given value of a. The following graph shows the graph of the original equation in the xa plane and the graph of a = 1 and a = -1.
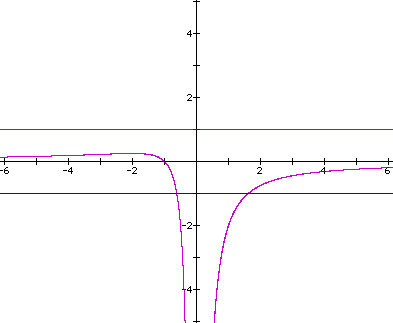
We can see that when a = 1, there are no roots for the original equation. When a = -1, there are two real roots for the equation, one positive and one negative. If we take the maximum value of the function
we find the largest value of a that will result in a graph of a parabola of the equation
with the parabola intersecting the x-axis in at least one point. The maximum value of a for which this occurs is a = .25. This means that the equation above will have no real solutions for values of a > .25. This can be observed by looking at the graphs of the equation for a parabola shown above for values of a = -3, -2, -1, 0, 1, 2, 3.
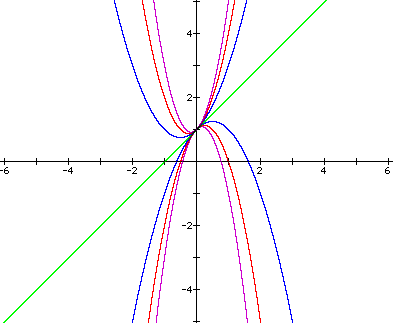
Now we consider the equation
where the value of b = -1 instead of 1, and we can characterize the roots of this equation for various values of a by graphing the relation
in the xa plane as shown below.
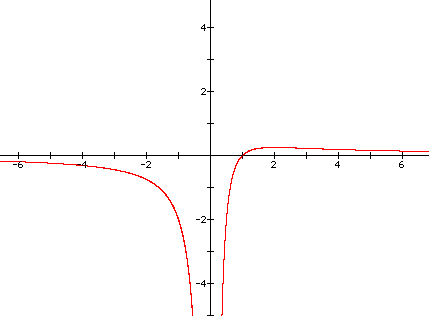
From the graph we can see that there are again no real solutions to the original equation for values of a > .25.
Now we will consider again the equation
and then graph this relation in the xb plane. This results
in the following graph.

Similarly to the graph in the xa plane, if we take a particular
value of b, say b = 5, and overlay this equation on the graph
we add a line parallel to the x-axis. If it intersects the curve
in the xb plane the intersection points correspond to the roots
of the original equation for that value of b. We have the following
graph.

Because the graph of each value of b is a horizontal line,
we can determine the characteristics of the roots of the original
equation for each possible value of b by observing the intersection
of the graph of the horizontal line with the graph of the relation
in the xb plane. It is clear on a single graph that we get two
negative real roots of the original equation when b > 2, one
negative real root when b = 2, no real roots for -2 < b <
2, One positive real root when b = -2, and two positive real roots
when b < -2.
Consider the case when c = - 1 rather than + 1 as shown by the
red graph.

Again each value of b that is selected generates a horizontal line. It is clear for this graph that there is one negative and one positive real root for all values of b.
We have already demonstrated that graphs in the xa and xb planes
can be used to show limiting values for the coefficients a and
b that will result in equations that have real solutions. Now
we will consider graphs in the xc plane. For this investigation
the equation
is considered. If the equation is graphed in the xc plane,
it is easy to see that the curve will be a parabola. For each
value of c considered, its graph will be a horizontal line that
intersects the parabola in 0, 1, or 2 points -- the intersections
being at the roots of the orignal equation at that value of c.
In the following graph, the graph of c = 1 is shown. The graph
illustrates the fact that the equation
will have two negative roots -- approximately -0.2 and -4.8.
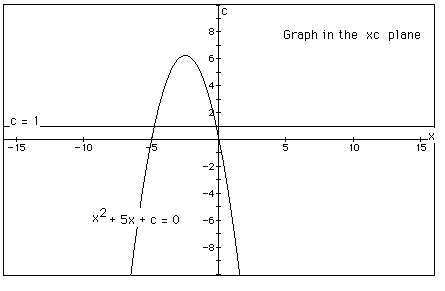
We can see that the vertex of the parabola is the one value of c where the equation will have only 1 real root, and this occurs as at c = 6.25. For c > 6.25 the equation will have no real roots and for c < 6.25 the equation will have two roots, both negative for 0 < c < 6.25, one negative and one equal to zero when c = 0, and one negative and one positive when c < 0.
Further explorations can be done using graphs in the xa, xb,
and xc plane to determine more about the nature of the roots of
quadratic equations. Students might want to explore some of the
following questions: