
Assignment #5
by Carol Sikes
The Library of Scripts
Introduction
In this write-up I present my Library of GSP Scripts. Scripts
are useful tools for performing frequently used constructions
when provided with a minimal amount of given information. For
each of the scripts provided, I will identify the givens required.
Segments of Equal Length
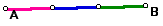
Trisecting A Segment - Given the
endpoints of the segment and a random point not on the segment.
Golden Ratio Segment (Divides
segment into two portions that form a golden ratio) - Given the
endpoints of the segment.
Centers of Triangles
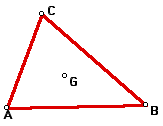
Orthocenter - O - Given the three
vertices of the triangle.
Incenter - I - Given the three
vertices of the triangle.
Triangle Centers (Orthocenter -
H, Centroid - G, Circumcenter - C, and Incenter - I) - Given
the three vertices of the triangle.
Circles of Triangles
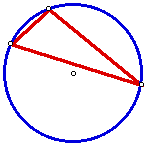
Incircle - Given the three vertices
of the triangle.
Triangles of Triangles
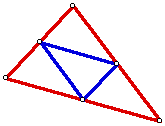
Orthic Triangle - Given the three
vertices of the triangle.
(The triangle formed from the midpoints of the segments
from the vertices to the orthocenter)
- Pedal Triangle - Given the three
vertices of the triangle and a distinct point P, the Pedal Point.
Polygons
- Isoceles Triangle - Given the
endpoints of the base and the endpoints of a segment representing
the desired altitude.
- Square - Given the endpoints of
one side.
- Pentagon - Given the endpoints
of one side.
- Pentagon - Given the endpoints
of a radius.
- Hexagon - Given the endpoints of
one side.
- Octagon - Given the endpoints of
one side.
Other Constructions
- Arc of Circle - Locus of the vertices
of a fixed angle that subtends a fixed segment - Given the vertex
of the angle and the endpoints of the fixed segment it subtends.
- Tangent Circle 1 - Construct a
circle externally tangent to two other circles given the centers
of the two circles and a point on each circle.
- Tangent Circle 2 - Construct two
circles tangent to a circle and a line given two points on the
line, the center of the circle and a point on the circle.





