

In this write-up, I examine constructions related to the orthocenters of triangles. First I will consider a triangle and look at the relationship between tthe orthocenters of the three triangles formed with the orthocenter of the original triangle and two of its vertices. Next I will look at the circumcircles of these three triangles and the original triangle. Finally I will look at some relationships between the circumcircle of a triangle and the altitudes or angle bisectors of the triangle.
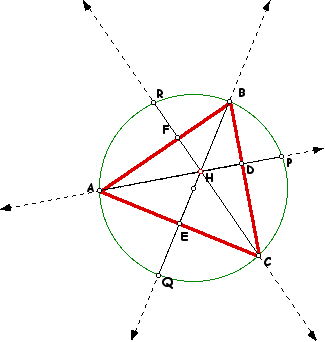
Consider a triangle ABC.
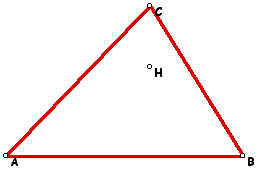
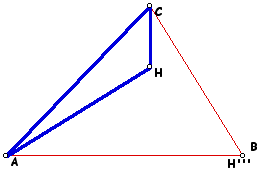
To construct the orthocenter of triangle ABC, the first step is to construct the altitudes of each side of the triangle. The point at the intersection of the altitudes is the orthocenter. The orthocenter is point H in the figure below. To use a Geometer's Sketchpad script to create a triangle and its orthocenter from three points, click here.
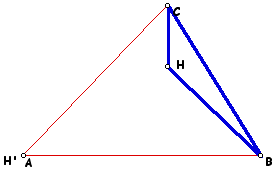
If the orthocenter H' of triangle HBC is constructed, it is located at vertex A.
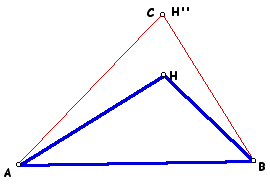
Likewise, the orthocenter H'' of triangle HAB lies at vertex C, and the orthocenter H''' of triangle HAC lies at vertex B.
When the circumcircles of triangle ABC, HBC, HAB, and HBC are constructed, this results in the four circles shown below.
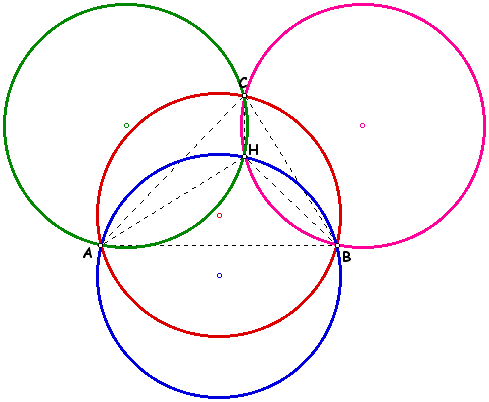
These four circles appear congruent. An extension of this investigation would be to prove that this is true.
If a vertex of triangle ABC is moved to the location of the orthocenter of ABC, then the new orthocenter would be located at the former position of the vertex. For example, if point A was moved to the location of point H in the figure above, then point H (the orthocenter of ABC) would be located where point A originated.
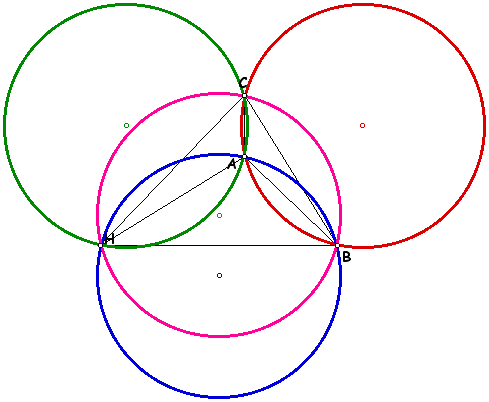
To experiment with moving these vertices using GSP, click here.
Consider a triangle ABC with its altitudes constructed and its circumcircle. The altitudes are extended so that they intersect the circumcircle and these points of intersection are constructed. A triangle DEF is constructed from these intersectios. The Orthic triangle JKL is constructed from the feet of the altitudes to give the following figure.
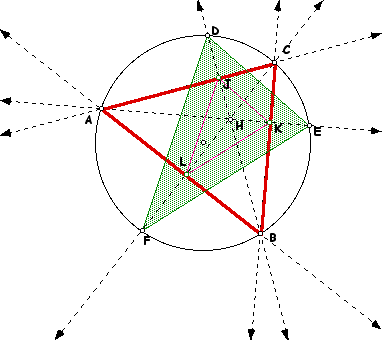
It can be seen using GSP that triangle DEF has an area that is four times the area of the Orthic triangle. If triangle ABC is an obtuse triangle, this relationship does not always exist.
For this figure, the following relationship can be seen using GSP:
I have not proved this conjecture, but that would be an interesting extension of the investigation of orthocenters.
One final observation is related to the angle bisectors of a triangle and the triangle's circumcenter. Given triangle ABC, the circumcircle is constructed and the angle bisectors of angles A, B, and C are constructed. The points where the angle bisectors interesct the circumcircle are constructed as shown below.
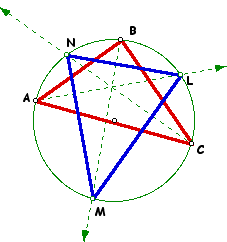
The intersection points L, M, and N are used to construct a triangle. The measures of the angles of this triangle can be related to the angle measures of the original triangle by the following relationships:
Angle L = 1/2 (Angle B + Angle C)
Angle M = 1/2 (Angle A + Angle C)
Angle N = 1/2 (Angle A + Angle B)
This relationship exists for all triangles, whether they are acute, right, or obtuse.
A possible activity for students would be exploring the construction to find the relationship between the angles L, M, N and A, B, C. Further extension of this activity could be to prove the relationship.