In this write-up, I examine the circumcenter of a triangle. I will discuss how the circumcenter is constructed and some of the properties of the circumcenter. I will also prove that the perpendicular bisectors of the sides of a triangle are concurrent.
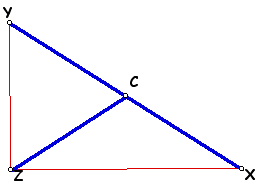
Consider a triangle XYZ.
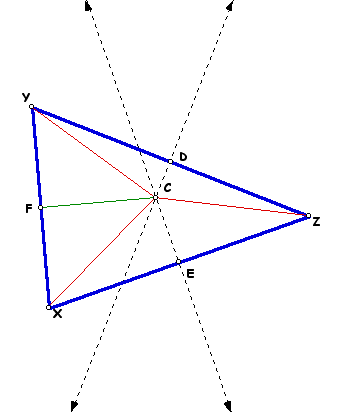
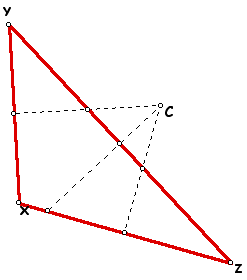
To construct the center of triangle XYZ known as the circumcenter, the first step is to construct the perpendicular bisector of each side of the triangle. The point at the intersection of the perpendicular bisectors is the circumcenter. The circumcenter is shown as point C in the figure. Because C lies on the perpendicular bisectors of the sides of the triangle, it is equidistant from each of the vertices.
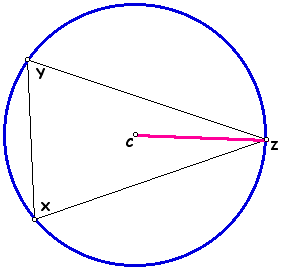
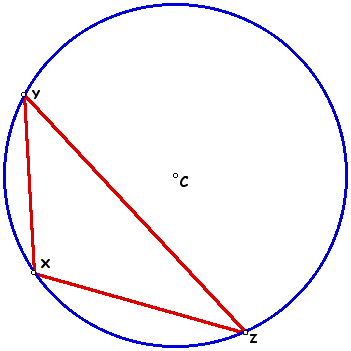
Point C is known as the circumcenter because it is the center of the circle circumscribed about the triangle through the vertices. The radius of the circle is formed between any of the vertices and the circumcenter C. The circumscribed circle demonstrates the property that point C is equidistant from each of the vertices of the triangle.
The location of the circumcenter and the position of the triangle in the circumcircle is dependent on whether the triangle is acute, right, or obtuse. For an acute triangle, the circumcenter lies inside the triangle.
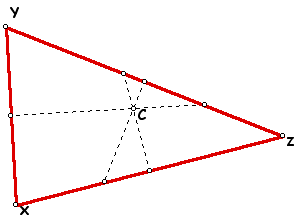
The acute triangle is found in both halves of the circumcircle.
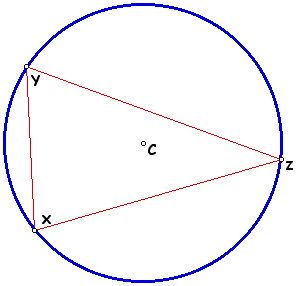
When triangle XYZ is a right triangle, the circumcenter lies at the midpoint of the hypotenuse. The hypotenuse of the triangle is the diameter of the circumcircle, and the triangle lies in only one half of the circle.
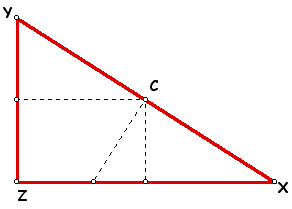
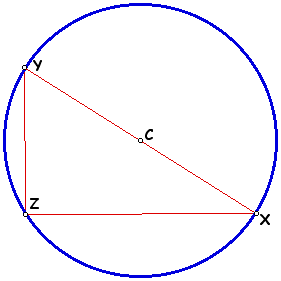
For obtuse triangles XYZ, the circumcenter lies outside of the triangle. Obtuse triangles are found in less than one half of the circumcircle.
If the segments between the vertices of an acute or obtuse triangle XYZ and its circumcenter are formed, three triangles are created.
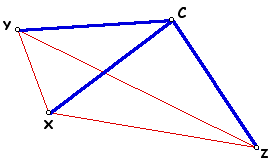
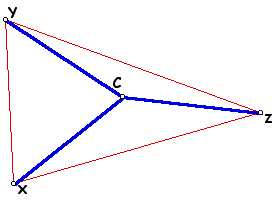
Triangles XCY, YCZ, and ZCX are isosceles, because two of the sides of each triangle are radii of the circumcircle.
These segments constructed for a right triangle form two isosceles triangles.
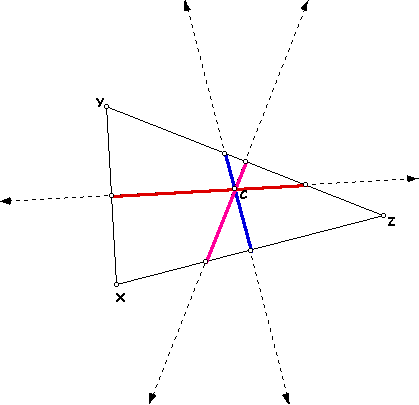
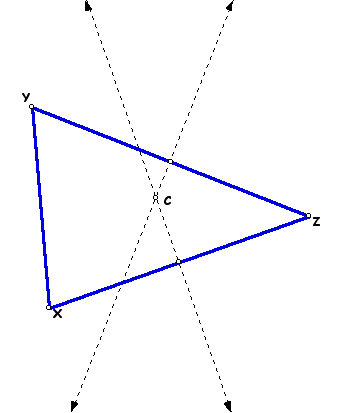
The circumcenter is the intersection of the three perpendicular bisectors of the sides of a triangle. In order to prove that that these three lines intersect at the same point, it is important to remember a key property of the perpendicular bisector: all points that lie on the perpendicular bisector of a segment are equidistant from the two endpoints of the segment.
First the perpendicular bisectors of two sides of triangle XYZ are constructed.
These two lines intersect at point C. The goal is to prove that the perpendicular bisector of YX also passes through point C. Next the segments between C and the vertices of the triangle are constructed. The midpoint of YX is constructed and also the segment between C and this midpoint F.
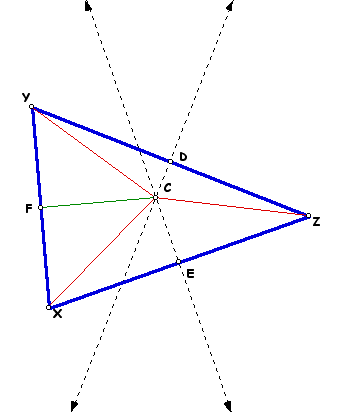
Because EC is the perpendicular bisector of XZ, CX and CZ are the same length. Because CD is the perpendicular bisector of YZ, CY and CZ are the same length. By transitivity, CX and CY are also the same length. Since F is the midpoint of YX, YF and FX are the same length. Since CF is the same length as itself, triangles CFY and CFX are congruent by side-side-side congruence.
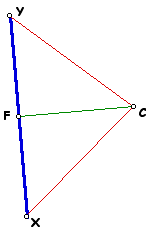
With CFY and CFX congruent, angle YFC is congruent to CFX. Angle measures are additive, therefore angle YFC + angle CFX is equal to angle YFX. Since the angle measure of a line segment is 180o, the measure of angle YFX is 180o. With angle YFC = angle CFX and angle YFC + angle CFX = 180o, 2*(angle YFC) = 180o so angle YFC = angle CFX = 90o.
The line segment CF bisects segment YX by construction, and it is perpendicular to segment YX as shown by the congruent triangles. Therefore segment CF lies on the perpendicular bisector of segment YX.