In this write-up, I explore the relationship between pedal triangles and to a given triangle based on the location of the pedal point.
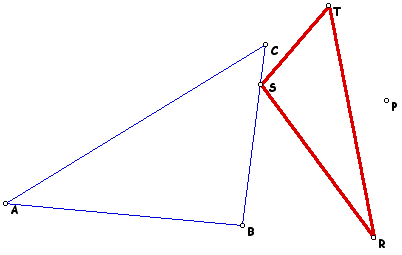
Consider a triangle ABC and a point P in the plane. This point P is known as the pedal point, and the pedal triangle is constructed from the intersections of the perpendiculars through P to the sides of triangle ABC. To use a GSP script to create a Pedal triangle given a triangle ABC and a point P, click here. In the figure shown below, triangle RST is the Pedal triangle of ABC for point P.
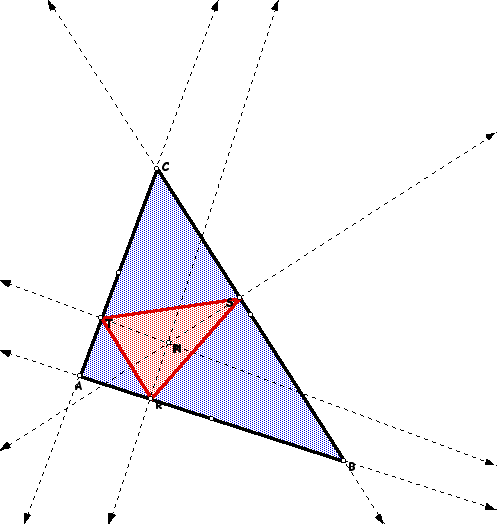
The location of the Pedal triangle changes as the point P is moved around in the plane. When P lies outside the circumcircle of ABC, at least some portion of triangle RST is external to triangle ABC. When P lies on the circumcircle of ABC, points R, S, and T become colinear and RST is a degenerate triangle. If the point P lies inside the circumcircle, at least some portion of triangle RST is internal to ABC. When P lies on the sides of triangle ABC or inside ABC and ABC is an acute triangle, triangle RST is internal to ABC. When ABC is an obtuse triangle, this is not always true. To experiment using GSP to demonstrate the effects of moving the point P to different points in the plane, including some of the centers of triangle ABC, click here. The Pedal triangle when P is the center of the nine-point circle is shown below.
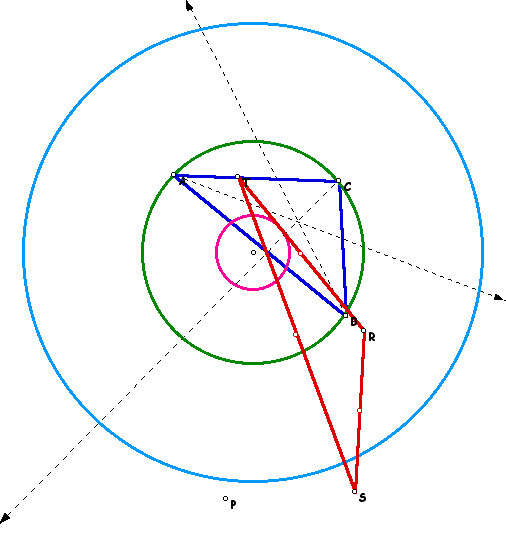
The loci of the midpoints of the sides of Pedal triangles formed when P lies on a circle that is concentric to the circumcircle are ellipses. This is true even when P lies on the circumcircle, and the Pedal triangle becomes the Simson line. Based on my observations in GSP, I have made several conjectures concerning these ellipses:
To observe the loci of midpoints of the Pedal Triangle formed when P is moved about one of the three circle shown below, click here.
As mentioned above, when the Pedal point lies on the circumcircle of triangle ABC, the Pedal triangle is a degenerate triangle. Points R, S, and T are collinear and they form what is known as the Simson line. There are some interesting properties related to the Simson line.
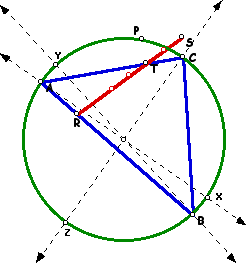
The first conjecture is related to the Pedal points on the circumcircle that produce Simson Lines that are concurrent with one of the sides of the triangle ABC.
For example, refer to the figure below:
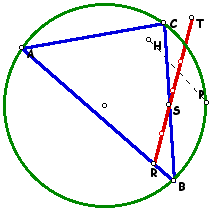
Next we consider a Pedal Triangle with P located on the circumcircle and the line segment constructed between P and the Orthocenter of ABC, point H.
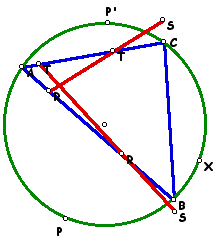
And finally we look at the intersection of two Simson lines created from separate Pedal points located on the circumcircle of triangle ABC. Let P, P', and X be three distinct points on the circumcircle as shown below.