

The following problem is posed on the Intermath website:
Suppose you want to build a rectangular fence against a natural boundary so that only three sides of fencing are needed (this means the fourth side is the natural boundary, like a cliff or a river). If you have a fixed amount of fencing, how should you build the fence so that you maximize the area of the enclosed region?
This essay explores the solution to this problem via the solution of a simpler problem solved using algebra and then illustrated using a GSP simulation to model the quadratic.
In order to solve this problem, first we will consider the problem of maximizing the area of a rectangular region with a fixed perimeter.
Algebraicly, we represent the fixed perimeter as 2P, with the one side of the fence having length X and the other having length P - X. This means that the area of the rectangular region equals:
![]()
or multiplying through yields the following:
![]()
Since this area function will result in a parabola that opens downward, then the maximum area occurs at the vertex of the parabola which is found by completing the square to yield the vertex form of the parabola:
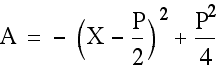
which yields the vertex 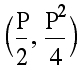
A Geometer's Sketchpad Investigation can be used to find the solution to the problem.
The students can then vary the location of point C along segment AB and as they record the length of AE and the corresponding area of the rectangle. This table of values can then be used to generate a graph of the length of one side of the rectangle versus the area of the rectangle. The graph will show a maximum at the vertex of a parabola, corresponding to the point where the rectangle is a square.
Click here to see a GSP Investigation of this problem.
Click here to see a graph of the table values generated from the investigation.
From the earlier investigation, we know that the maximum area of the rectangular region enclosed by a fixed amount of fencing occurs when the area is a square. Therefore if you have a fixed amount of fencing (F) and a natural boundary of length N, then there are three possible scenarios.
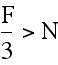
For this situation, there is more than enough fencing to create a square of side length N. Therefore, add N and F and divide this sum by four to yield the best possible side length for the fence.
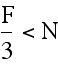
For this situation, there is not enough fencing to create a square of side length N. This means that two of the sides of the rectangle will have length N and the other two will have a length equal to (F - N) divided by two.
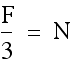
The simplest of the cases, there is exactly enough fencing to create a square of length N. This will yield the maximum area for the fencing.