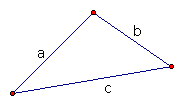
Consider a triangle ABC as shown below:

First the altitude h from the vertex opposite c is constructed.

Now side c is divided into two sections, one of length x and the other of length c - x as shown.
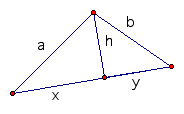
We can use the Pythagorean theorem to find h in terms of a, b, x, and y.
For the different parts of the triangle, we have that:
(1) ![]()
(2) ![]() and
and
(3) ![]() by construction
by construction
Considering that the area = ![]() , then
the area squared =
, then
the area squared = ![]() , so
, so ![]() .
.
Rearranging equation (3) and substituting into equation (2) yields the following result:
![]()
Subtracting this result from equation (1) yields:
![]()
Rearranging equation (1) and multiplying through by ![]() yields
the following:
yields
the following:
![]() which factors into
which factors into
![]() where
where ![]() gives
the following:
gives
the following:
![]() which can be rearranged to yield:
which can be rearranged to yield:![]()
Since ![]() , this equation becomes:
, this equation becomes:
![]()
Factoring out the two's and dividing on both sides results in this equation:

Taking the square root of both sides results in Heron's formula for the area of a triangle:
![]()