By nami Youn


Write-up  #1

Exploring graphs of y= asin(bx+c)

for differen values a, b, and c.

Introduction

In this write-up, I examine the graphs of y=asin(bx+c) for different values a, b, and c.

First, I fix the values of "b" and "c" at 1 and examine what happens to the graph as I vary the values of "a". Then, I fix the values of "a" and "c" at 1 and examine what happens to the graph as I vary the values of "b". Finally, I fix the values of "a" and "b" at 1 and examine what happens to the graph as I vary the values of "c.

I note the whole changes in the graphs of y=asin(bx+c) as I vary the values a, b, and c.

1. Varying the values of "a"

1) Let b=1 and c=1. Then let's compare the graphs of y=asin(x+1) when a=0.5, 1, 2, and 3.
 
 

y=0.5sin(x+1)(purple curve) y= sin(x+1)(blue curve)

y= 2sin(x+1) (yellow curve) y=3sin(x+1) (green curve)
 
 







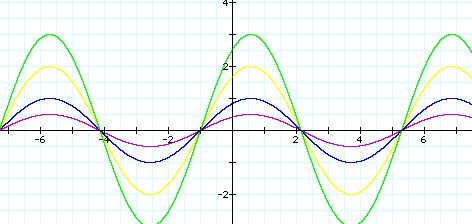
 Let's notice the amplitude of each graph.
On the graph, a ranges from 0.5 to 3. As a increses, the graph has more maximum and minimum points.
 
 
maximum value of the graph 
         minimum value of the graph
y = 0.5sin(x+1)
o.5
-0.5
y= sin(x+1)
1
-1
y = 2sin(x+1)
2
-2
y = 3sin(x+1)
3
-3

 

Therefore, changing a affects the amplitude, maximum and minimum points of the graph y= asin(bx+c)

Also, the smaller the values of a , more "spread out" the graph appears. That is, as a increases, the graph appears more compressed.
 

2)  Now, let's look at the graphs of y=asin(x+1) when a=2 and -2, especially, a is negative.

y= 2sin(x+1) (yellow curve)

y= -2sin(x+1) (green curve)
 
 
 
 






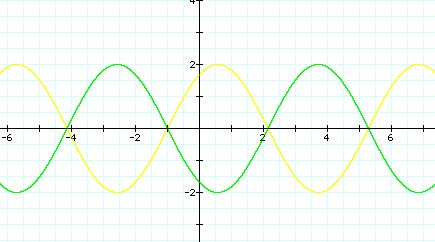
Again, the amplitude has been changed to a. But, the  range of the graph of two graphs  is the same, from -2 to 2.

If a is negative, -2, the graph is flipped. Therefore, the value of affects the concavity of the graph of y= asin(bx+c)
 
 


2. Varying the values of "b"


 1 ) Let a=1 and c=1. Then let's compare the graphs of y=sinbx+1 when b=0.5, 1, and 2.
 
 

y=sin(0.5x+1)(purple curve)     y= sin(x+1)(blue curve)    y= sin(2x+1) (yellow curve)
 






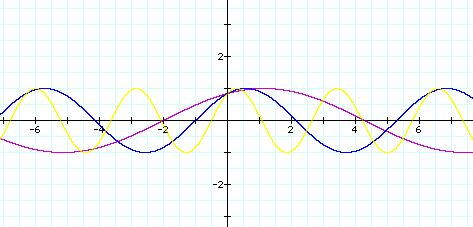
Let's notice the period of each graph.

Compare the periods of two graphs in case b=1(blue) and b=2(yellow).
We can notice that within one period of the graph when b=1, there are two peroids when b=2.

Again, compare the periods of two graphs in case b=0.5(purple) and b=2(yellow).
We can notice that within one period of the graph when b=0.5, there are four peroids when b=2.

Therefore, as b decreses, the periods of the y= asin(bx+c) increases, so the graph appears to smooth.
But, the maximum and minimum values are not changed.
 


2)  Now, let's look at the graphs of y=sinbx+1 when b=2 and -2, especially, a is negative.
 
 

y= sin(2x+1) (yellow curve)

y= sin(-2x+1) (green curve)
 
 
 







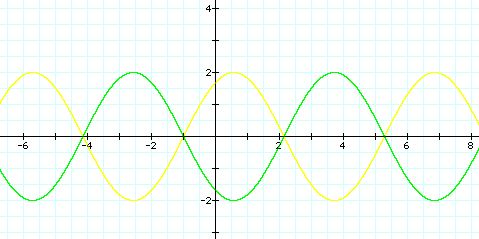
First, let's notice the period of each graph.

The period of two graphs is exactly the same. That means that the graph still has two periods within b=1. But, the graph when b=-2 has been shifted to the right.
 


3. Varying the values of "c"

Let a=1 and b=1. Then let's compare the graphs of y=sinx+c when c=-1, 0, 1, and 2.
 
 

y =sin(x-1)(purple curve)         y = sinx(blue curve)

y = sin(x+1) (yellow curve)     y =sin(x+2) (green curve)
 
 




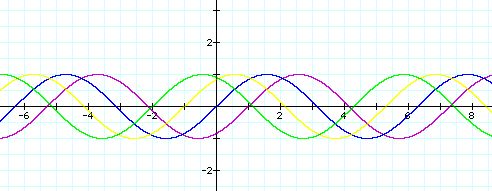
When c is positive, we can see that the graph shfit to the left and across the y-axis when y = -c.
Again, when c is negative, the graph shifts to the right and across the y-axis when y = c.

Therefore, varing the value of c shifts the graph to the left or right .

Extension

Now, try to predict how the following graphs will look like.

y = -sinx

y = 2 sin( x -1)

y = -4 sin( 3x+1)

y = 0.5sin(-x - 2)
 
 

Return to Nami's Home Page