By Nami Youn


Write-up  #10


Parametric Curves

Introduction

A parametric curve in the plane is a pair of functions

x = f(t)
                                                                    y = g(t)

Where  the two continuous function define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve.The curve is dependent on the range of t.

In this write-up, I will investigate the parametric equations and variation of these equations.

                                                                   x = acos(t)
                                                                   y = bsint(t)  for various a and b
 

1. For a equals to b,            x = acos(t)
                                          y = bsint(t)

First, let's consider the case a, b > 0.

a = b = 1 (purple),    a = b = 2(blue),    a = b = 4(green)





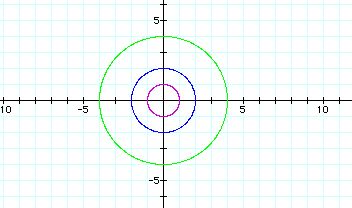
We can notice that the all graphs are the circles centered at the origin(0, 0). Specially, for a = b = 1, the graph is the unit circle. The radius are 1, 2, 4 respectively, the same value as a =b.
So, we  can see that the value of a=b decides the radius of the circle, the graph of x = cost (t), y = sin(t). Also, as the value of a=b increases, the radius of the circle is greater.


Next, let's consider the case a, b < 0.
 
 

a = b = -1 (purple),    a = b = -2(blue),    a = b = -4(green)






We can get the same graphs as the case a, b>0.  Notice that the all graphs are also the circles centered at the origin(0, 0). Specially, for a = b = -1, the graph is the unit circle. The radius are 1, 2, 4 respectively, the same as the absolute value of a =b.
So, we  can see that the absolute value of a=b decides the radius of the circle, the graph of x = cost (t), y = sin(t). Also, as the absoulte value of a=b increases, the radius of the circle is greater.

We have another result through investigation of the graphs. If the absoulte values of a and b of two equations are the same, the two graphs are exactly equal. For example, the graphs of both x = cost (t), y = sin(t) and x = -cost (t), y = -sin(t) are the same.

2.  For a does not equal to b,            x = acos(t)
                                                          y = bsint(t)


Next, let's consider the case the absolute value of  a <  the absoulte value of b
Let fix a = 1 varing the value of b.
 
 

b = -2(purple),  b = 3(blue),  b = 5(green)




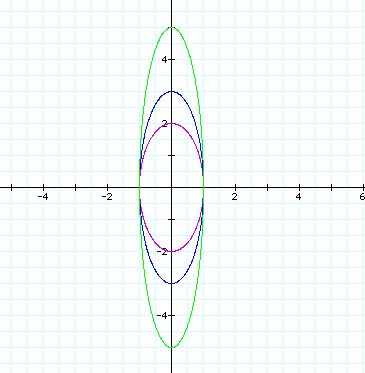
It is obvious that the graphs are ellipes. The center of the all ellipes is the origin(0, 0).
Also, we can notice that the graph is enlongated along the y-axis as the absoulte value of b increases.


Next, let's consider the case the absolute value of  a >  the absoulte value of b
Let fix b = 1 varing the value of a.
 
 

a = -2(purple),  a = 3(blue),  a = 5(green)




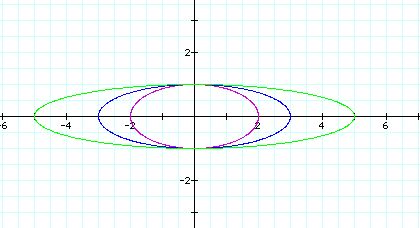
We have the different shape of ellipes. But, the center of the all ellipes is still the origin(0, 0).
We can notice that the graph is enlongated along the x-axis as the absoulte value of a increases.

To the top

Return to Nami's Home Page