
By Nami Youn

By Nami Youn
Write-up #11
Polar Equation
Introduction
In this write-up, I will investigate ![]() varing a, b, c and k.
varing a, b, c and k.
a= -4(purple), -2(blue), 1(green), 3(yellow), 5(gray)
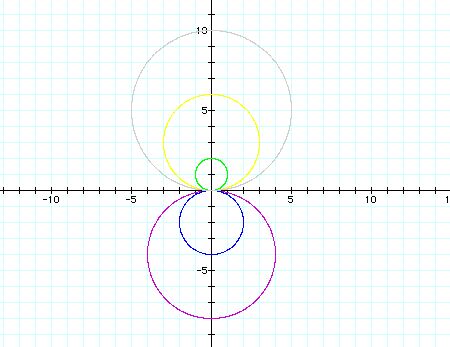
we can get the circular graphs for values of variable
a.
The value of a determined the radius of the circle. As
the absolute value of a increases, the radius is greater.
If a>0, the circle lies below the x-axis.
If a<0, the circle lies above the x-axis.
a. Let the value of k be 2. This means the case k = even
a= -4(purple), -2(blue), 1(green), 3(yellow),
5(gray)
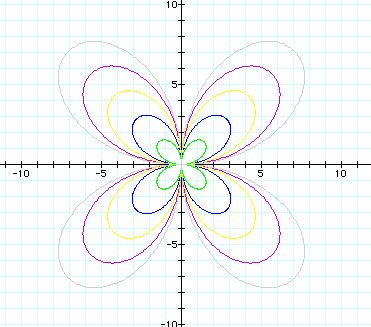
Each graph has four petals. The number of petal = 2k.
The absolute value of a determines the size of the petals.
The four petals looks the same one another. Also, one
petal is obtained from reflection of the other petals over y = x , x-axis
or y-axis.
a= -4(purple), -2(blue), 1(green), 3(yellow), 5(gray)
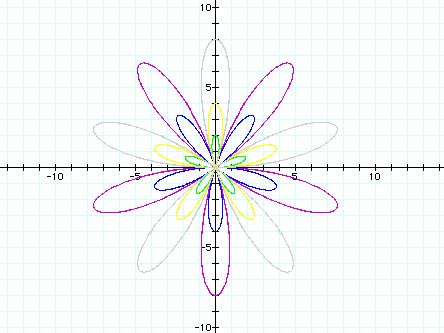
Each graph has five petals. The number of petal = k.
The absolute value of a determines the size of the petals.
The five petals looks the same one another.
k = 1.5(purple), 3.5(blue)
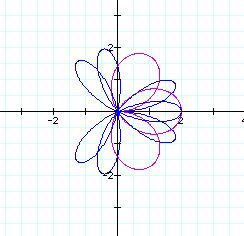
The number of petals are 3 and 7 respectively. Each number
is two times k petals.
Then, what is difference between the graphs of
the case k = 1.5 and k = 3 or the graphs of the case k =3.5 and k
=7.
See and compare the following graphs.
k =1.5(purple), k =3(blue). k = 3.5(green), k = 7(black)
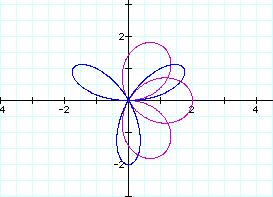
The two graphs of k =1.5 and k = 3 are not the same. The
size and location are different.
But, the number of petals are the same.
Also, as the number of petals increases, their graphs
become narrow.
a= -4(purple), -2(blue), 1(green), 3(yellow), 5(gray)
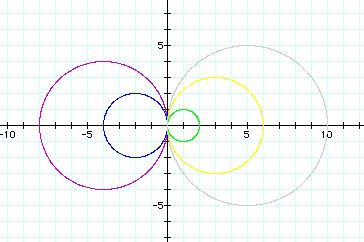
we can get the circular graphs for values of variable
a.
The value of a determined the radius of the circle. As
the absolute value of a increases, the radius is greater.
If a>0, the circle lies to the left of the y-axis.
If a<0, the circle lies to the right of the y-axis.
a =4(purple), a=8(blue),
a=12(green)
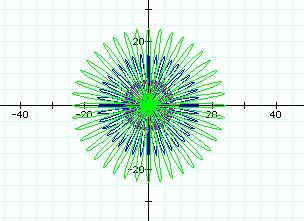
As the value of a increases for the larger value k, the number of petals is the exactly same, but the legnth of the petals is longer..
2) Varing k
Since the pattern of the petals are the same as sine equations,
let's examine the graphs varing k in the case of the constant a=2.
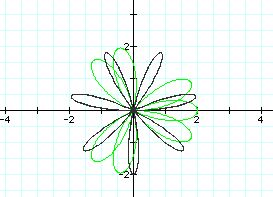
k=2(purple), k=5(blue), k=3.5(green)
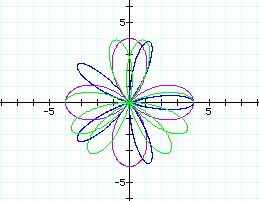
we have the following results.
when k = 2 (even integer), the number of petals is 4 =
2(k)
when k = 5 (odd integer), the number of petals
is 5 = k
when k =3.5( not integer), the number of petals is 7
= 2(k)
Let the values of a and k be fixed 1
b = -5(purple), b=-1(blue), b=0(green), b=4(yellow), b=8(gray)
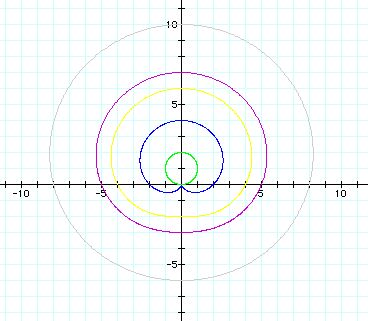
As the absolute value of b increases, the graph looks
more like a circle.
The y-intercept of the graph is 2+b. For example, if
b=8, y-intercept is 2+8.
b = 1(purple), b=3(blue), b=8(green), b=16(yellow)
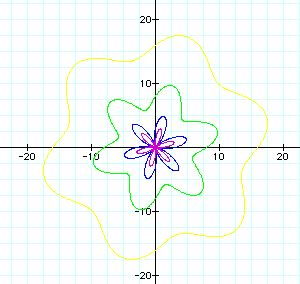
All graphs have 6 petals. As the value of b increases, the graph is spread(streched) apart from the origin(0,0). So, the graph looks more like a circle. This means that the petal is fatter.
b = 500(purple), b=1000(green)
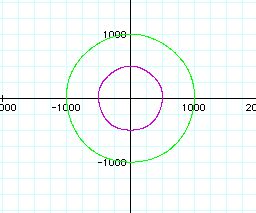
As the value of b increases, the graph looks more like a circle.
b = -5(purple), b=-1(blue),
b=0(green), b=4(yellow), b=8(gray)
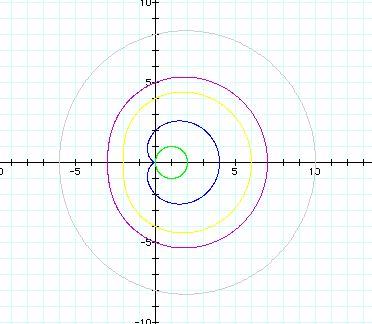
As the absolute value of b increases, the graph looks
more like a circle.
The x-intercept of the graph is 2+b. For example, if
b=8, x-intercept is 2+8.
b = 1(purple), b=3(blue), b=8(green), b=16(yellow)
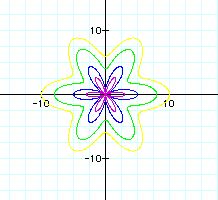
All graphs have 6 petals. As the value of b increases,
the graph is spread(streched) apart from the origin(0,0). So, the graph
looks more like a circle. This means that the petal is fatter.
Wow! These graphs are the exactly same as r= 2asin(kt)+b.
b = 500(purple), b=1000(green)
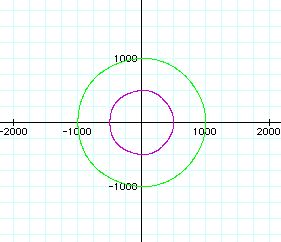
As the value of b increases, the graph looks more like
a circle.
These graphs are the exactly same as r= 2asin(kt)+b.
c = -5(purple), c = -1(blue), c= 2(green), c = 4(yellow)
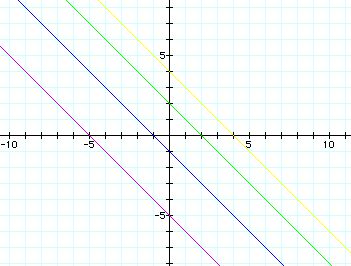
The graphs are the lines. The value of c means the x-intercept.
k = 4(purple) k= 6(blue)
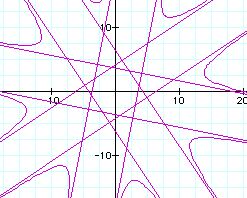
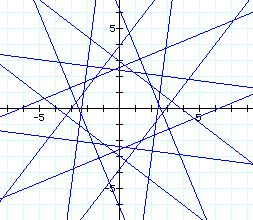
k = 5(green) k= 7(sky)
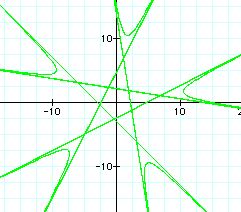
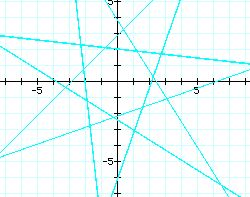
when k= even, the graph has a polygon with 2k-sides.
When k= odd, the graph has a polygon with k-sides.
For k = 4, the graph has 2(4) sided figure.
For k = 5, the graph has 5 sided figure.