Write-up  #4

Investigating centers of a Triangle

The Circumcenter and the Centroid of a Triangle
 
 

Introduction

In this write-up, I examine some centers of a triangle; Thecircumcenter and the centroidof a triangle.

First, I construct the circumcenter and the centroid of a triangle using GSP. Then, I will explore each center's location for shapes of triangles and properties. Finally, I investigate the relation between the circumcenter and the centroid of a triangle.

1. Circumcenter

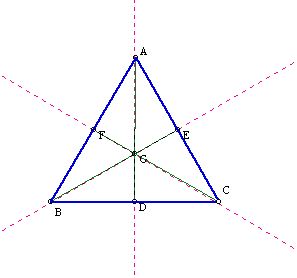
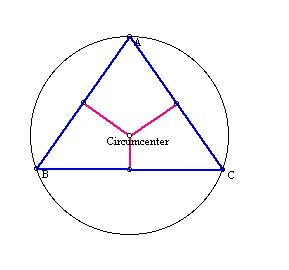
The circumcenter of a triangele is the intersection point of three perpednicular bisectors of each side in a triangle.


The circumcenter is the center of the circumcircle of the triangle.
 
 











Since triangles APC and BPC are congruent(SAS), triangles BNC and DNC (SAS) and triangles AMC and DMC, AC=BC=DC.

So, any circle with C as center and passing through one of the vertices will go through all of them.

The circle is called circumscribed circle(circumcircle).


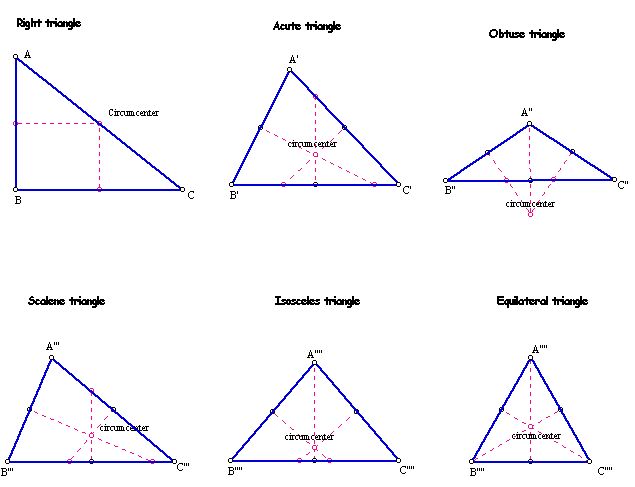
 where if the point of circumcenter is of a triangle?
 
 
   Inside  On side  Outside
 Right triangle   
 x
  
 Acute triangle
 x
    
 Obtuse triangle    
x
 Scalene triangle 
x or
 x or
x
 Isosceles triangle
x or
 x or
  x 
 Equilateral triangle
 x
    

 
 
 










2. Centroid


The definition of the median of a triangle is a line segment that extends from one vertex of a triangle to midpoint of the opposite side. The three medians all come together in one point, called the centroid of triangle ABC.


The centroid is always inside the triangle.
 
 
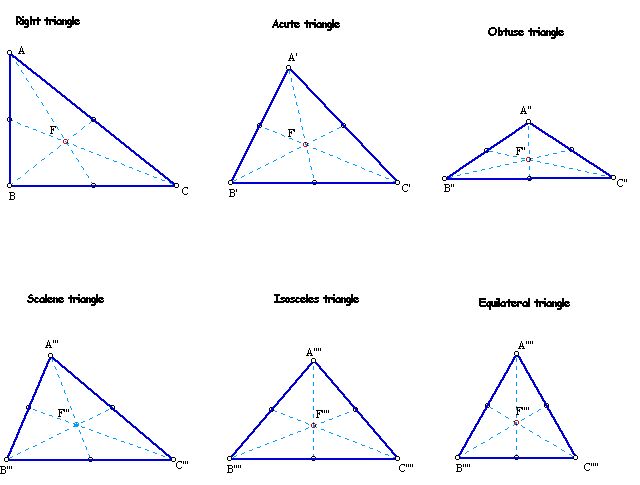
Inside Onside Outside
Right triangle  x
Acute triangle x
Obtuse triangle x
Scalene triangle  x
Isosceles triangle x
Equilateral triangle x

 






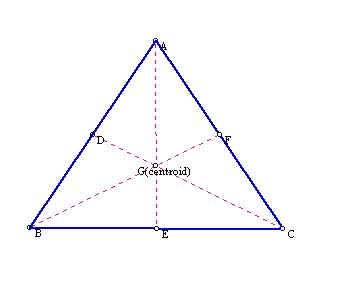
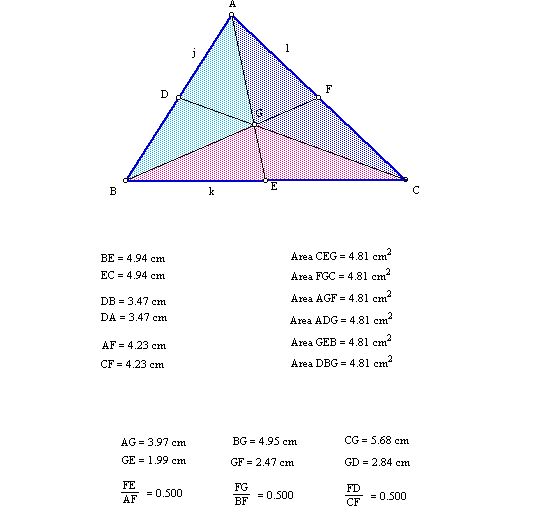
The interesting properties of the centroid

1) Distance
Centroid in a triangle divides each median into two parts, the ratio whose lengths is 2:1.

AF : FE = BF : FG = CF : FD = 2:1








2) Area
The six areas of the interior triangles formed by the three medians in the triangle are all the same.

area CEF= area GFC =area AFG= area = ADF= area FEB= area DBF
 










3. The relation between the circumcenter and the centroid

For an equilateral triangel, the circumcenter and the centroid are the same point(G).

 * perpendicular bisectors (pink dished line)
 * medians (green line)
 
 








To the top

Return to Nami's Home Page