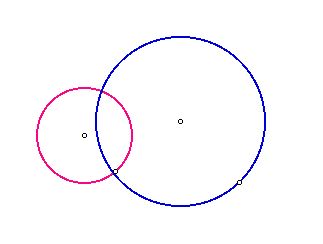
Given two circles and a point on one of the circles. We construct a circle tangent to the two circles with one point of tangency being the designated point D.
First of all, we should think of three cases accrding to the position of two circles.

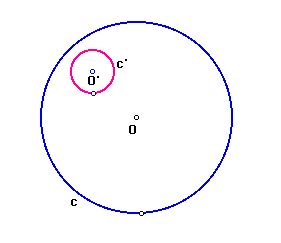
#1 Since the center of the desired circle will lie on a line through O the center of the given circle c, we can constuct the line through O.
 
 

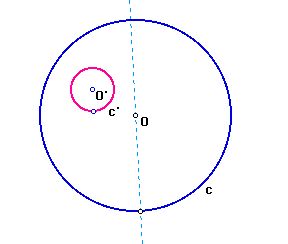
#2 We  construct a circle centered at F, whose radius is equal to the radius of c'. Connect the center of o' and an endpoint of  diameter of c''. Construct the perpendicular line to this segment. Then the center of desired circle is the intersection point of a perpendicular bisector of pink segment and the blue lay.
 
 

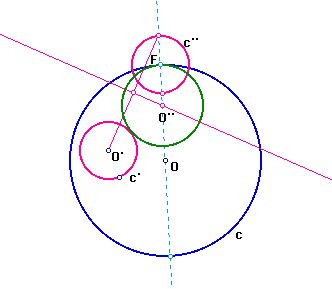
O'O'' + O'O = radius of c' + radius of c = constant. 

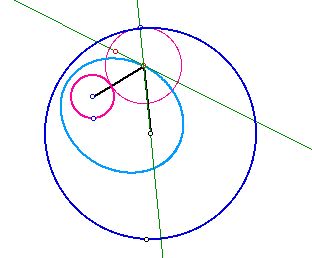
Click here for a GSP sketch to see a trace of the line as the tangent point of the constructed circle
moves around the large circle. An envelope of lines is produced all tangent to the ellipse.

The center of the desired circle will lie on the line through the center of the given circle  c'.
 
 

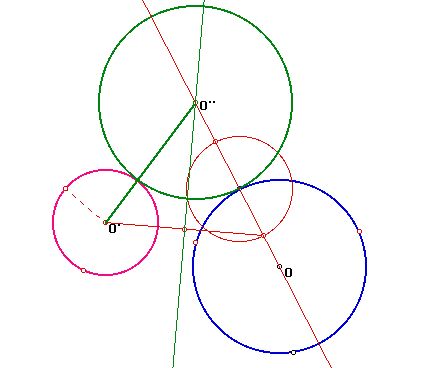
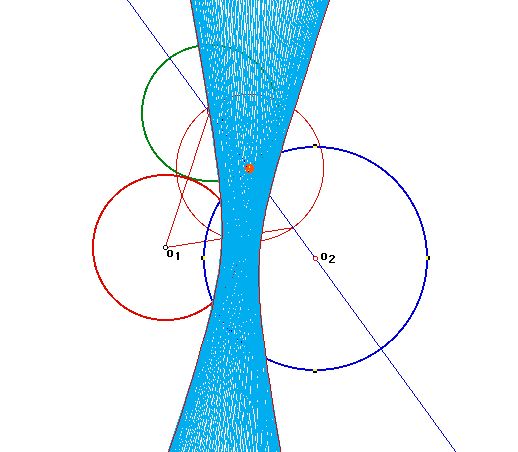
We can see O'O'' - OO'' = radius of c + radius of c' = constant.
Therefore, the locus of the centers of the tangent circles is an hyperbola with foci at the centers of the given circles.
Click here for a GSP sketch.

To the top

Return to Nami's Home Page