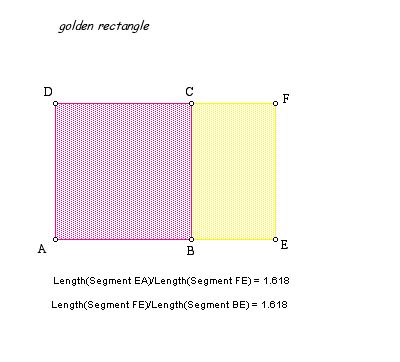
The Golden Rectangle has been said to be one of the most visually satisfying of all
geometric forms. We can find many examples  in art masterpieces such as in edifices of ancient Greece.

GSP file

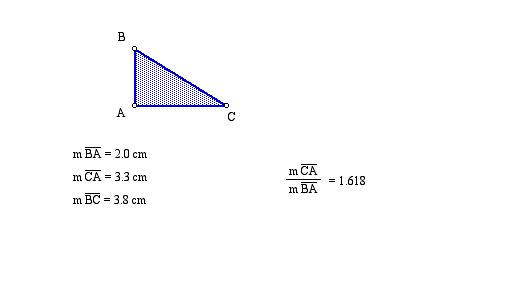
If we rotate the shorter side through the base angle until it touches one of the legs, and then, from the endpoint, we draw a segment down to the opposite base vertex, the original isosceles triangle is split into two golden triangles. Aslo, we can find that the ratio of the area of the taller triangle to that of  the smaller triangle is also 1.618…. (=Phi)
 
 

The Golden Spiral above is created by making adjacent squares of Fibonacci dimensions and is based on the pattern of squares that can be constructed with the golden rectangle.
 
 

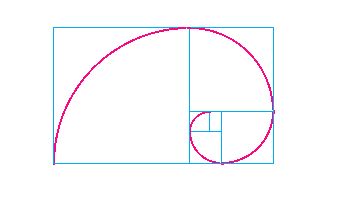
If you take one point, and then a second point one-quarter of a turn away from it, the second point is Phi times farther from the center than the first point. The spiral increases by a factor of Phi.

This shape is found in many shells, particularly the nautilus.
 
 

The British physicist and mathematician, Roger Penrose, has developed an aperiodic tiling which incorporates the golden section. The tiling is comprised of two rhombi, one with angles of 36 and 144 degrees (figure A, which is two Golden Triangles, base to base) and one with angles of 72 and 108 degrees (figure B).
 
 

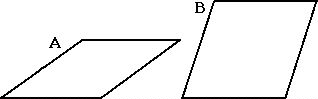
When a plane is tiled according to Penrose's directions, the ratio of tile A to tile B is the Golden Ratio.
 
 

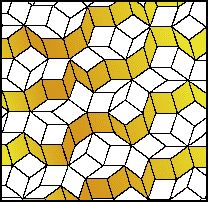
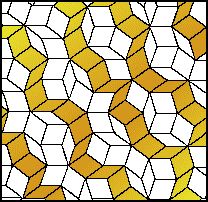
In addition to the unusual symmetry, Penrose tilings reveal a pattern of overlapping decagons. Each tile within the pattern is contained within one of two types of decagons, and the ratio of the decagon populations is, of course, the ratio of the Golden Mean.
 

We can see there are lots of lines divided in the golden ratio. Such lines appear in the pentagon and the relationship between its sides and the diagonals.
 
 

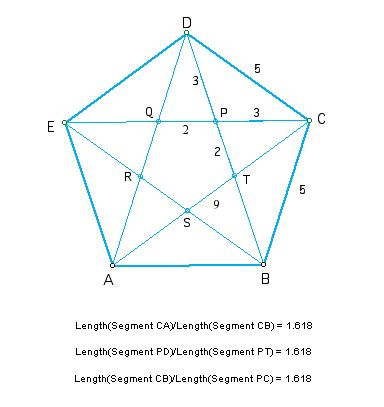
We can get an approximate pentagon and pentagram using the Fibonacci numbers as lengths of lines. In above figure, there are the Fibonacci numbers; 2, 3, 5, 8. The ratio of these three pairs of consecutive Fibonacci numbers is roughly equal to the golden ratio.