Tessellations and Escher by Lindsay Allen

Maurits Cornelius Escher (1898 - 1972) is known for his "impossible drawings", drawings using multiple vanishing points, and his "diminishing tessellations". Throughout his various art work, Escher uses complex mathematics, inparticular, geometry. Here we will focus on tessellations... what is a tessellation? How did Escher use tessellations?

(Click HERE to see a complete history of M. C. Escher.)

Tessellations are divisions of the plane; more precisely, they are closed shapes that cover the plane. The word is derived from the Latin word "tessella", which were small square stones or tiles used in ancient Roman mosaics. All tessellations can be classified as those that repeat, are non-periodic, quasic-periodic, and those that are fractals. The tessellations that fall in the repeating category can then be classified as being regular (which consists of three types) or semi-regular (which consists of eight types).

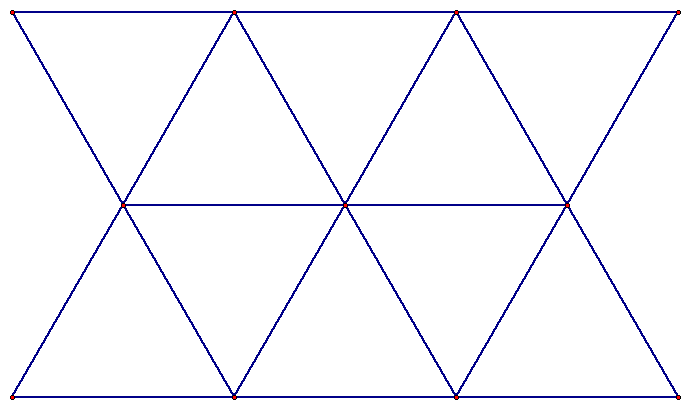
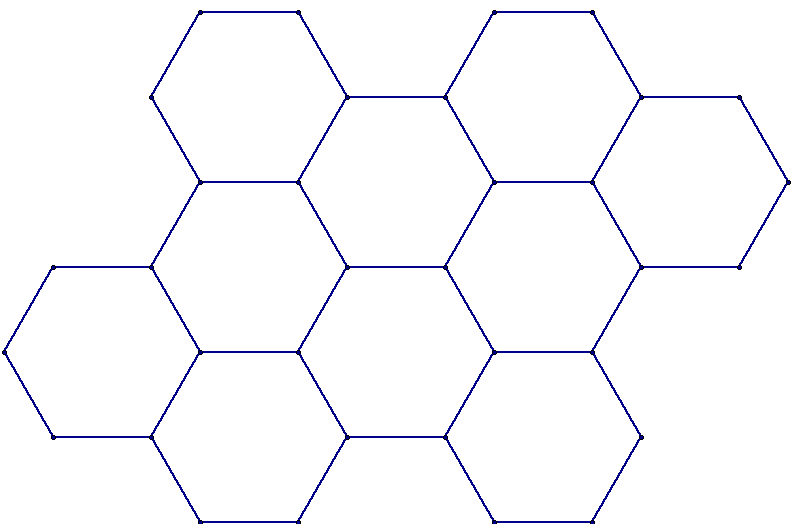
There are only three regular shapes that can "tessellate", or tile a plane... the triangle, square, and hexagon. Each of these tessellations consists of the same type of regular polygon.

"Liberation"

"Day & Night"

"Reptiles"

Escher created these tessellations using reflections, translations, rotations, and a combination of the three. To see how to do this, click on the links below.

REFLECTIONS TRANSLATIONS ROTATIONS

There is a software program that allows you to create your tessellations. Tesselmania! uses translations, rotations, and glide reflections to construct the tessellations. Click HERE to learn more about Tesselmania!.

Escher is not only known for his awesome tessellations. He also had many works closely related to polyhedra. Click HERE to visit a website on Escher and Polyhedra.

LINKS

History and Overview of Escher and His Works:

http://www.brown.edu/Students/Catalyst/fall2001articles/features/kumar-escher.html

http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Escher.html

http://www.etropolis.com/escher/notes1.htm

Mathematical Discussions of Escher's Work:

http://www.geocities.com/davidschow/HUB/escher.htm

http://members.tripod.com/vismath/dunham/

Tessellations:

http://www.porcelainia.com/tess.html

http://library.thinkquest.org/16661/escher/tessellations.1.html

Lesson Plans:

http://ccins.camosun.bc.ca/~jbritton/jbescher.htm

http://www.sasked.gov.sk.ca/docs/midlmath/escher.html

http://www.geom.umn.edu/apps/gallery.html

http://www.math.csusb.edu/courses/m129/eqtri.html

http://plato.acadiau.ca/courses/educ/reid/4183/TAs/activities/Final_Project.htm

http://ccins.camosun.bc.ca/~jbritton/jbsymteslk.htm

Other Extremely Helpful Sites:

http://www.mathacademy.com/pr/minitext/escher/index.asp

http://www.sd91.bc.ca/webquests/tessellations/escher.html

To Purchase Escher Prints:

http://www.WorldOfEscher.com/gallery/

(NOTE: All of the above websites were used to create this page.)

Return to my HOME PAGE