We will examine what happens to the quadratic equation
as the variable d varies.
1) First off we'll start with d = 0. We will call this our base graph.
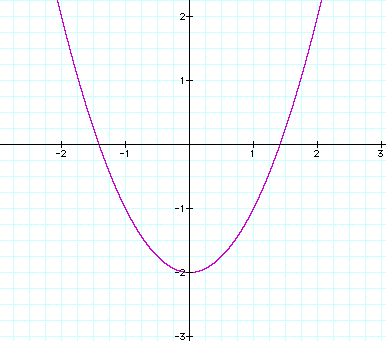
Where does the vertex seem to be on this graph? Make sure to verify your estimate. Where are the x-intercepts? Make sure to verify your answers.
2) Now we'll change d to 2 and observe what happens.
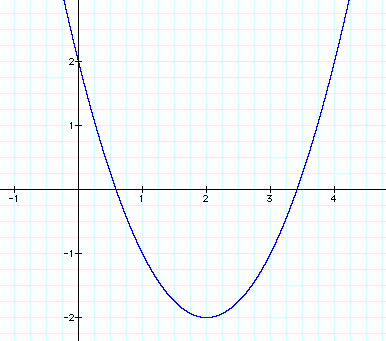
Careful, the positon of the origin has changed. Where is the vertex now? Estimate the x-intercepts. Make sure to verify all guesses either graphically or algebraically.
Describe the difference in the grpahs of the two parabolas.
3) Next, we'll set d = 4. Before we do that though, answer the following questions:
a) Where do you think the vertex will be?
b) Where do you think the x-intercepts will be?
Here's a link to the graph with the previous two graphs. The new graph is red. Did your answers hold? If not, adjust your answers as necessary.
4) Now, you've seen three graphs already. What about negative numbers? Make a conjecture of where the base graph will be when d = -3.
5) Describe what will happen to
6) To check your answer to question 5, here's a video of the parabola as d varies from -5 to 5. Here's the Graphing Calculator file. As always, Graphing Calculator can be purchased from www.nucalc.com.
For those who absolutely haved to have the answers, they are here.
This page last edited on 4 November 2002.