PARAMETRIC EQUATIONS
Manipulating the Parametric
Circle
by Laurel A. Bleich
A parametric curve in the plane is a
pair of functions
x = f(t)
y = g(t)
where the two continuous functions define
ordered pairs (x,y). The two equations are usually called the
parametric equations of a curve. The extent of the curve will
depend on the range of t and your work with parametric equations
should pay close attention the range of t . In many applications,
we think of x and y "varying with time t " or the angle
of rotation that some line makes from an initial location.
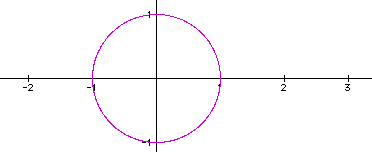
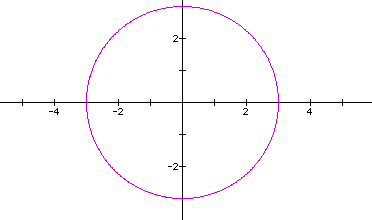
The parametric circle has the equation:
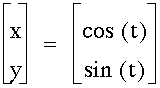
Taking the range of t to be 0 to 2pi,
as t increases a circle is constructed counter-clockwise around
the origin:
for 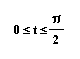 , the graph is
, the graph is
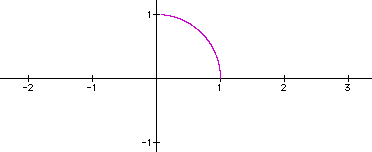
for  , the graph is
, the graph is
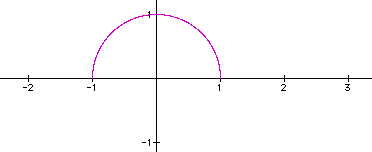
so then for 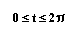 , we have the circle
, we have the circle
In what ways can we manipulate this
equation though?
Take the equation: 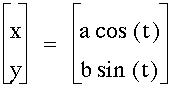 , and vary values of a and b. What would
you expect to get? This in fact becomes the parametric equation
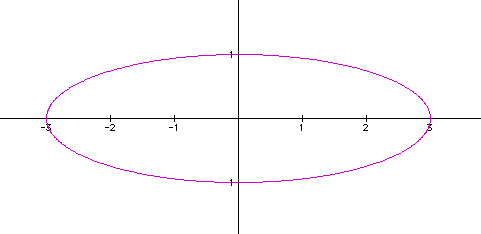
for an ellipse. For a=3, b=1, the following graph is constructed:
, and vary values of a and b. What would
you expect to get? This in fact becomes the parametric equation
for an ellipse. For a=3, b=1, the following graph is constructed:
CLICK HERE
to view this equation in Graphing calculator and change the values
of a and b.
Notice that when a = b, we get a circle
again. In the following graph a=b=3:
What about the equation 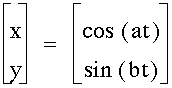 ?
?
Let a = 2, and change the value of of
b?
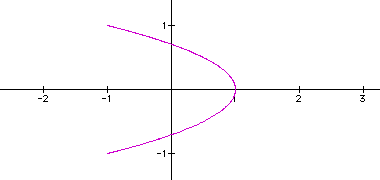 for b=1,
for b=1, 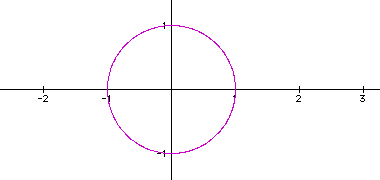 for
b=2.
for
b=2.
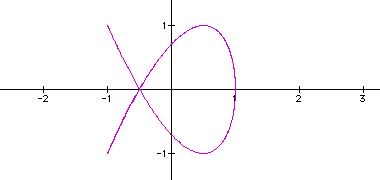 for b=3,
for b=3,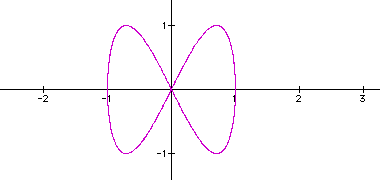 for
b=4
for
b=4
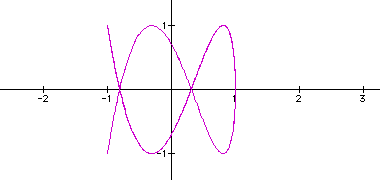 for b=5,
for b=5, 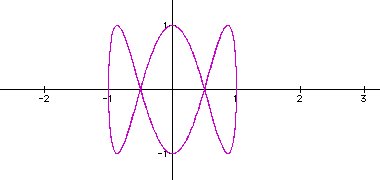 for
b=6
for
b=6
The first thing I notice is that when
a|b (a divides b) the graph is closed. And it seems that the value
is the number of loops the graph will have. And when is a doesn't
divide b, the graph isn't. Also notice again that when a=b, we
get a circle.
Is this always the case?
Click here
for when a=4, and the range of b is set from 0-20. Once again,
the graphs that are closed are the ones when 4|b and when a=b
the graph is a circle.
What can we say when we hold b constant
and vary a? Let b = 2.
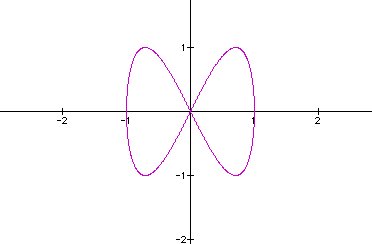 for a=1,
for a=1, 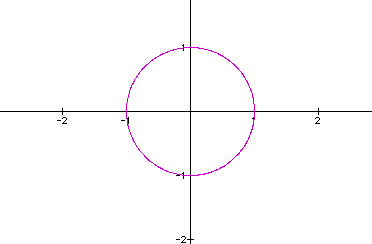 for
a=2,
for
a=2,
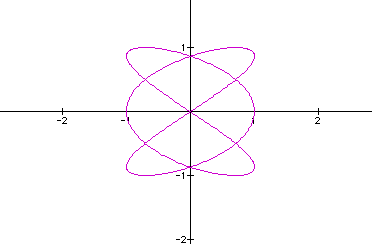 for a=3,
for a=3, 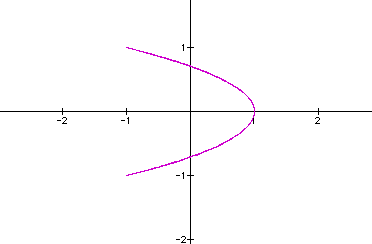 for
a=4
for
a=4
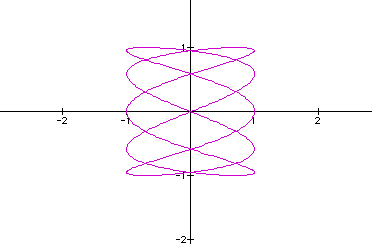 for a=5,
for a=5, 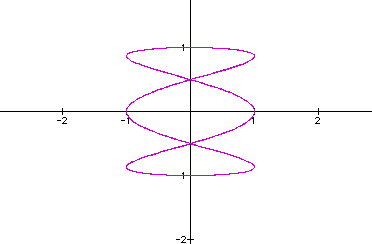 for
a=6
for
a=6
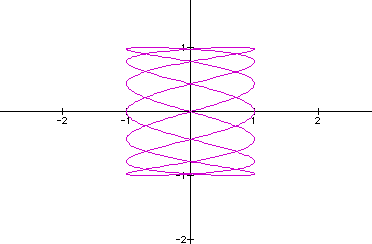 for a=7
for a=7 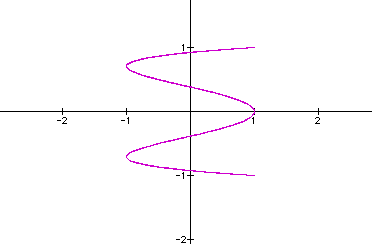 for
a=8
for
a=8
Looking at additional values of a, I
noticed that when b doesn't divide a, the graph is closed and
the number of (veritcal) loops is equal to a.
When b does divide into a, there are two different outcomes. When
the quotient is even, then the graph is open, but if the quotient
is odd, then
the graph is closed. And noticed once again when a=b, the graph
is a circle.
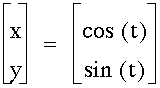
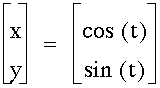
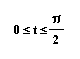 , the graph is
, the graph is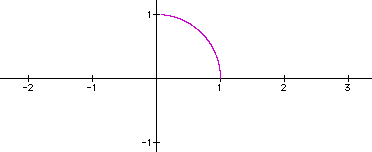
 , the graph is
, the graph is
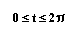 , we have the circle
, we have the circle
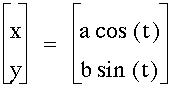 , and vary values of a and b. What would
you expect to get? This in fact becomes the parametric equation
for an ellipse. For a=3, b=1, the following graph is constructed:
, and vary values of a and b. What would
you expect to get? This in fact becomes the parametric equation
for an ellipse. For a=3, b=1, the following graph is constructed:

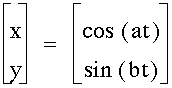 ?
? for b=1,
for b=1,  for
b=2.
for
b=2.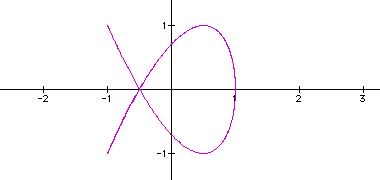 for b=3,
for b=3, for
b=4
for
b=4 for b=5,
for b=5,  for
b=6
for
b=6 for a=1,
for a=1,  for
a=2,
for
a=2, for a=3,
for a=3, 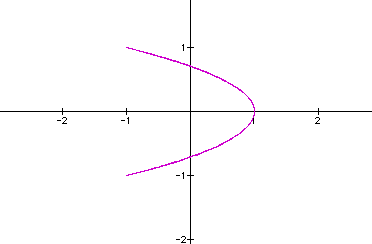 for
a=4
for
a=4 for a=5,
for a=5,  for
a=6
for
a=6 for a=7
for a=7 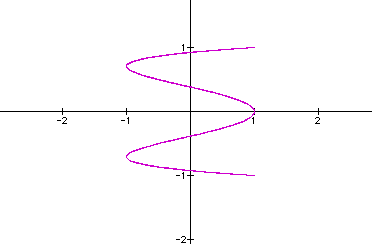 for
a=8
for
a=8