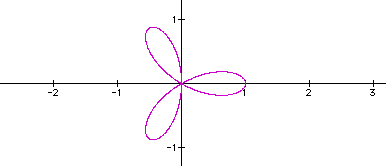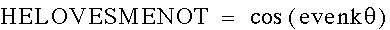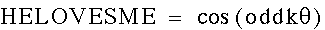POLAR EQUATIONS
"He Loves Me/He Loves Me
Not"
by Laurel A. Bleich
Every little girl at one time or another has played the game
"He Loves Me/He Loves Me Not" where for each pedal she
would pull off the flower, she would alternate her responses for
her representation of the pedal (i.e. "He loves Me' or "He
Loves Me Not")
saying letting fate determine if "Tommy" likes her
or not.
Well, by using a little math and polar equations, she can
instead of letting 'fate' determine if he loves her, her can choose
her own.
So the question is given the two choices: He Loves Me, and
He Loves Me Not, can we predetermine how many pedals a flower
must have to get the desired outcome.
We look to polar equations in the form of 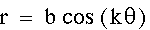 to help us figure out which flower
to pick to get our desired outcome.
to help us figure out which flower
to pick to get our desired outcome.
To begin with, let's graph the polar equation while holding
b constant at 1 and varying k.
When k=2:
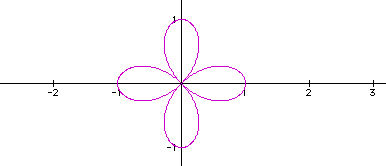
When k=3:
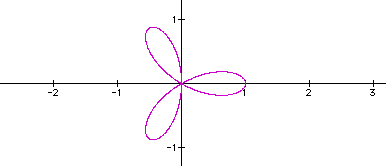
When k=4:
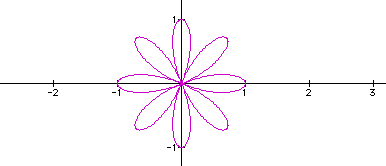
When k=5:
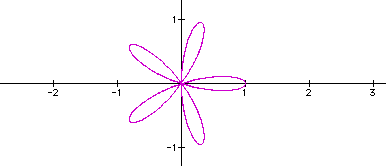
When k=6:
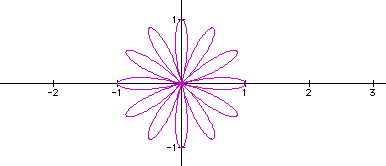
From the above pictures, one can conclude that as 'k' changes,
the number of pedals change. To view more 'flowers', at different
values of k, CLICK HERE for a movie.
So for what values of 'k' do you want to get the desired outcome.
When 'k' is odd, the number of pedals will be the value of 'k',
and when k' is even, the number of pedals will be 2*k.
There are two outcomes - "He Loves Me" or "He
Loves Me Not" - how many pedals would you want if you wanted
the outcome to be "He Loves Me", when the first pedal
pulled is "He Loves Me"?
Starting with "He Loves Me", we have:
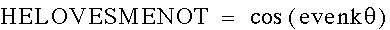
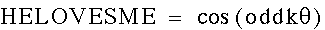
So depending on which outcome you want, you can pick your
flowers accordingly.
Does changing the value of 'b' change our above equations?
Remember we held 'b' constant at one. The following are graphs,
for various values of 'b', where k is constant at 6.
When b = 2:
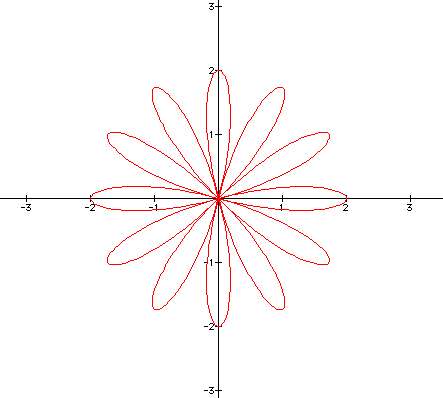
When b = 3:
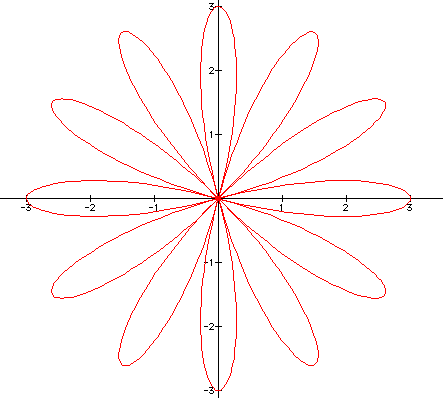
And when b = 4:
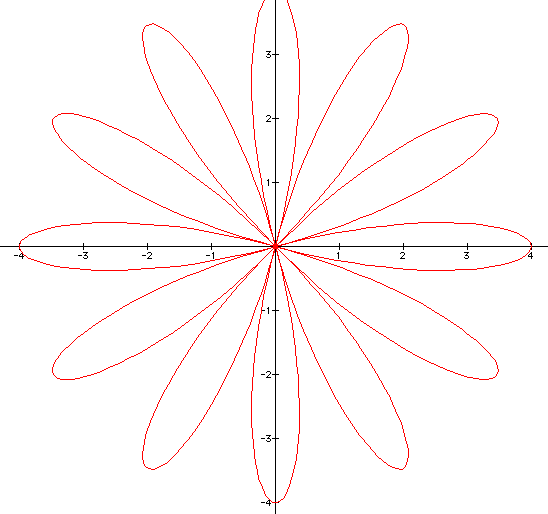
Thus, from the graphs, it seems that changing 'b' doesn't
change our original outcome. Changing 'b' only changes the 'length'
of the pedal.
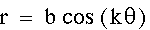 to help us figure out which flower
to pick to get our desired outcome.
to help us figure out which flower
to pick to get our desired outcome.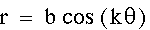 to help us figure out which flower
to pick to get our desired outcome.
to help us figure out which flower
to pick to get our desired outcome.