Various Relationships between a Triangle and its Medial Triangle

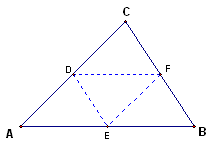
First recall that a Medial Triangle is the triangle constructed from the 3 midpoints of the sides of the original triangle.  The question that now arises it what kinds of relationships are there between these (two) triangles - are they similar, congruent, what's the area comparison, and ratio of their perimeters.   The following page explores these relationships for all types of triangles, i.e.. equilateral, isosceles, and right, as well as for any given triangle.

The following items will be compared in this write-up with the following triangle as the referenced triangle. 

Congruency? Similarity?
Length of Segments? Perimeter
Area?

CONGRUENCY?  SIMILARITY?

Are the four triangles created from the construction of the medial triangle congruent?

If we had an equilateral triangle, this would be obviously true.     For AD @ AE @ EB @ BF and <A @ <B, so triangles ADE and BFE are congruent by SAS.  And the following triangle CDF is congruent to the previous two by a similar argument.  What about the Medial Triangle though?  It also is congruent to the other three triangles?  Can you see how?

One way to show this is from our previous congruencies, DE @ EF @ DF.  So we have an equilateral triangle, which implies that all three angles are 60 degrees.  Additionally, take the triangle ADE. From the larger angle we know that angle A is 60 degrees.  And since D and E are the midpoints, triangle ADE is an isosceles triangle which implies angle ADE is congruent to angle AED; therefore they too are both 60 degrees.  Hence, triangle DEF too in congruent to the other three triangles.

What if the triangle isn't equilateral though?  What can we say about the congruency of these triangles now?    Let's take a look at just two segments of the medial triangle.  Since the segments that create the medial triangle are parallel to the segments of the original triangle, respectively,  we can conclude congruency of some of the angles.   (NOTE:  The number depicts the angle in reference and the word angle as well as the value of degrees will be left out for simplicity of the argument.) 

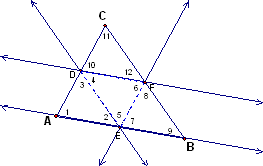
     Figure 1                                                                                Figure 2

Figure 3                                                                                       Figure 4

From the Alternating Angle Theorem, the following angles are congruent:

2 @ 4 @ 12 
3 @ 5 @  8
6 @ 7 @ 10

Additionally, since the sum of the degrees of a triangle is 180, we have the following:
(1)  1  +   2   + 3 = 180
(2)  4  +   5 +   6 = 180
(3)  7  +   8 +   9 = 180
(4) 10 + 11 + 12 = 180 

We can now substitute in into the above equations, the congruencies we found.   Take for example equation (1):
1 + 4 + 5 = 180.  From equation (2),  we know that 1 must be congruent to 6.   Likewise, for (3), we have
6 + 5 + 9 = 180, which implies 9 @ 4.  And for (4), we have 11 @ 5.  Thus, we have similar triangles.  

But do we have congruent triangles?    Since DE @ DE, we have triangle ADE  @ FED by ASA. And by a similar argument, the other triangles are congruent to the Medial triangle as well.  Hence they are all congruent to each other.

Similarity of the triangle ABC with the medial triangle? We showed above that the angles of triangle ABC are congruent to angles of the medial triangle DEF.  (need to verify order) 

Back to Top

 LENGTHS OF SEGMENTS? PERIMETER?

What about the relationship between the length of  DE in relation to AB?    We now need to draw upon the relationship of similarity that we just proved.   Similar triangles have their segments in the same ratio.  For example:

DF  =  DE  =  FE
AB      CB      CA

Recall that AB = AE + EB, AC = AD + DC; and BC = BF + FC.   And from the above congruencies, we know that 
AE @ DF
AD @ EF

From the above ratios - we can substitute in for the following:

   DF     =      DF       =     DF     =    1  
AE+EB        2(AE)         2(DF)         2

So the relationship between the lengths of the sides of the medial triangle to the larger triangle is 2: 1 (i.e if AB = 4, then DF = 2)

Therefore, the perimeter of the Medial, P(DEF) = (DE + DF + EF) and the perimeter of larger triangle, P(ABC) = (AB + BC + CA). Substituting in our ratio length,
P(ABC) = (2DF) + (2DE) + (2FE) = 2(DF + DE + EF). So the perimeter of the larger triangle is twice as large as the perimeter of Medial triangle.

Back to Top

AREA?

What about the area of the smaller triangle to the original?   Now that we know the length comparison, we can just plug our ratio in the Area of a Triangle Equation : A= 1/2(b*h).

First let's draw the altitudes for our triangles (height).

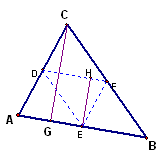
For the original triangle we have A 1/2 (AB * CG)  and for the Medial triangle we have  A = 1/2(DF*EH).   From our ratio of lengths (2:1) though,, we can deduce that the area of the smaller triangle is one fourth that of the original:

A = 1/2*[1/2(AB*CG)]  = 1/4(AB*CG)

Back to Top