" A pedal triangle for any triangle ABC, is the triangle, whose vertices are the feet of the perpendiculars from A, B, and C to the opposite sides of the triangle."
"When the pedal point, P, lies on the Circumcircle of any triangle ABC, the pedal triangle degenerates into a straight line known as the Simpson Line."
In this exploration, I want to examine what happens with the Pedal Point is set to the various Triangle Centers -
Circumcenter
Incenter
Orthocenter
Centroid
I have create a general GSP srcipt tool for the construction
of the pedal triangle where P can be located anywhere in the plane
of the triangle ABC.
CLICK HERE to view the script
tool.
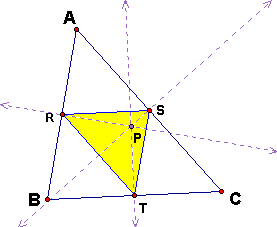
WHAT HAPPENS WHEN THE PEDAL POINT IS CIRCUMCENTER OF THE TRIANGLE ABC?
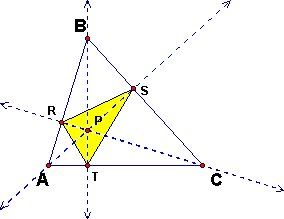
Let's first take a look at when P is inside the Triangle ABC:

If P is the circumcenter of Triangle ABC, then it lies on the
perpendicular bisector for each side of Triangle ABC. Then one
can speculate that P is the orthocenter
of Triangle RST. Recall that the orthocenter of a triangle is
the common intersection of the three lines containing the altitudes
(i.e PT perpendicular to RS.)
How did we arrive at this? Pedal point is perpendicular to the sides of Triangle ABC.
What happens though when the Circumcenter is located outside the triangle?
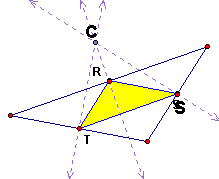
Even though the Pedal Point is outside the triangle, the Pedal Triangle still remains inside.
CLICK HERE to manipulate the location of the Pedal Point when it is the Circumcenter.
WHAT HAPPENS WHEN THE PEDAL POINT IS INCENTER OF THE TRIANGLE ABC?
In the following picture, we notice that P lies on the perpendicualar bisector of each one of its sides.
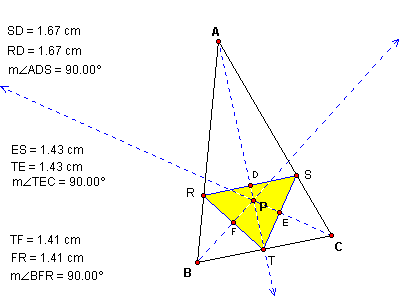
Therefore, it becomes its own circumcenter.
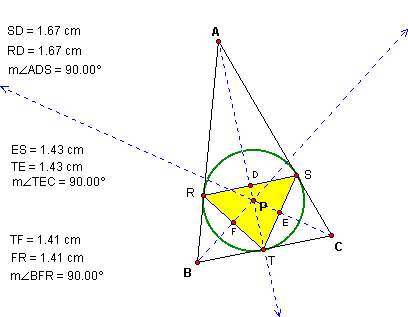
WHAT HAPPENS WHEN THE PEDAL POINT IS ORTHOCENTER OF THE TRIANGLE ABC?
P now lies on the altitudes to sides of Triangle ABC. P then becomes the incenter for Triangle RST - P lies on the angle bisector for the angles of the smaller triangle.
EXPLORE WHAT HAPPENS WHEN THE PEDAL POINT IN THE CENTROID OF THE TRIANGLE ABC?
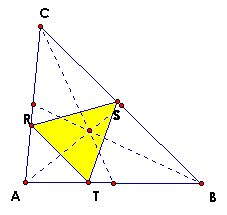
Click Here to explore when P is equal to the Centroid.