Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
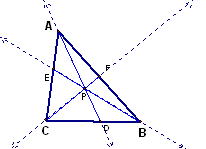
1.) What is the relationship between the triangles created? Can the result be generalized so the point P can be outside the triangle?
2.) Show that when P is inside triangle ABC, the ratio of the
areas of triangle ABC and triangle DEF is always greater than
or equal to 4. When is it equal to 4?
PART 1: What is the relationship between the
triangles?
What can you say about (AF)(BD)(CE) / (BF)(CD)(AE)?
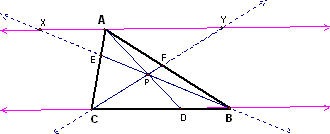 |
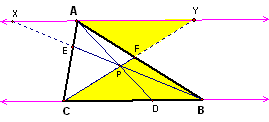
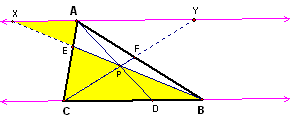
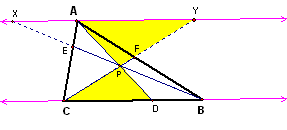
Draw a line through A that is parallel to BC and then extend the lines BE and CF to intersect this line at points X and Y, respectively. |
 |
 |
 |
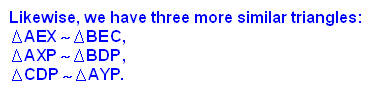 |
 |
 |
From all these similar triangles....we have various relationships:
What can be said about (AF)(BD)(CE) / (BF)(CD)(AE)?
In the table above in the last column, we notice that AX/BD
AY/DC which implies BD/DC = AX/AY.
Take the following and multiply them together:
AF/BF = AY/BC
CE/AE = BC/AX
BD/DC = AX/AY
(AF/BF)*(CE/AE)*(BD/DC) = (AY/BC)*(BC/AX)*(AX/AY) = 1.
(This result is Ceva's Theorem)
PART 2: Show that when P is inside
triangle ABC, the ratio of the areas of triangle ABC and triangle
DEF is always greater than or equal to 4. When is it equal to
4?
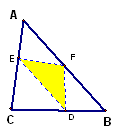
When the interior triangle is the medial triangle (when P is the centroid), the area of the ABC is 4 times as that of DEF. This was shown in an earlier exploration, Various Relationships between a Triangle and its Medial Triangle.
What if the triangle isn't the medial triangle? Click here to explore ratio of areas when P is anywhere inside ABC. No matter where P is, the area is greater or equal to 4.
Notice that when P moves away from the centroid toward any of the vertices, the ratio grows.
Return to Laurel's Homepage