The function y = sin (x) is what is known as a periodic function because it repeats itself at specific intervals called periods. In this exploration, we want to investigate 1.) what happens when we multiply sin x by a constant; 2.) what happens when we multiply the variable, x, by a constant and 3.) what happens when we add a constant to either the variable, x, or to the value of sin x.
Let's first define some terminology that we will be using in this exploration.
Periodic functions: a function whose values recur at fixed intervals as the variable uniformly increases.
Radians: 180/ pi
Cycle: a portion of the graph from one point on the graph to the next point where the graph starts repeating.
Period: the horizontal length of one cycle.
Amplitude: the distance from its axis to a high point or a low point.
Typically when we work with trigonometric functions we use radian measure. Why do we use Radian measure? (Due to the limitations of the graphing utility - all graphs in this exploration will show x-y coordinates)
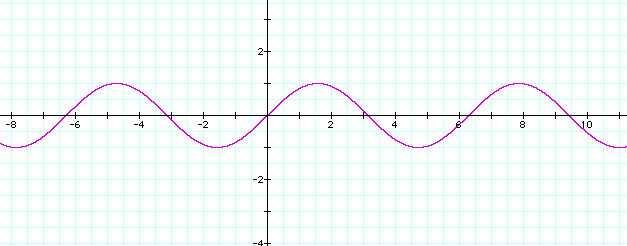
To begin with, let's graph the function y = sin x.
Analyzing the following graph below, we notice that
the next time the function begins to repeat itself is when x=
and y 0. Thus the period
is . So at every multiply
of , you will get y = 0.
Further observation, you notice that the amplitude of this curve is 1 - i.e. the greatest value of y will be 1.
The question that now arises is: what happens when we multiple the right hand side by a constant A - where A can be either positive or negative (For A=0, we get y=0; and for A=1 we get y=sin x. So for this argument, we want A<0 or A>1). So for the following values of A, let's graph the following functions.
For A = 2: y = 2 sin x ; For A = -4: y = -4 sin x; For A 1/2: y = 1/2 sin x.
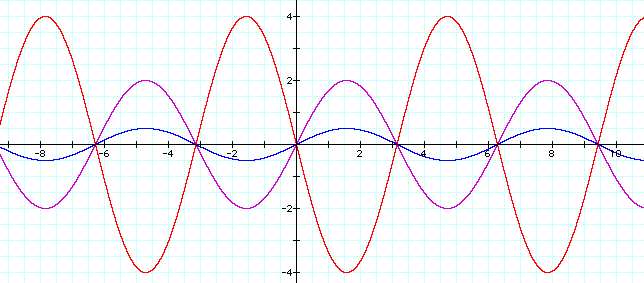
Basically, what is going on is that for the original value of y, we are multiply it by C, hence changing the amplitude of the curve.
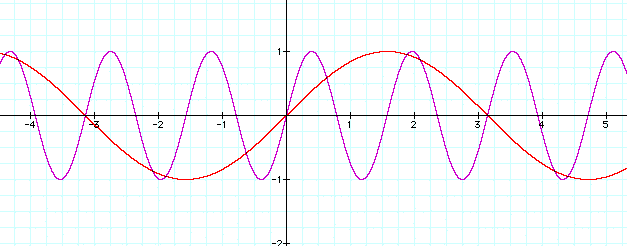
We know now how to change the amplitude of a the function y= sin x from the above case. But what if we want to change the period? Let us take any integer, B, and multiply it to x. Hence, we are multiplying the angle (in radians) of what we input to the sine function.
What happens when B is positive, when B is negative? Take a look at the movie to demonstrate what happens when B is equal to -4,-3,-2, -1, 0, 1, 2, 3, 4.
We conclude from watching the movie, that as B changes in value, the period changes. But how? As you may recall, the period for y sin x is (2*pi). When we multiply a constant, we are changing the period of the function to (2*pi/B).
So for the function y = sin 4x, our period is now pi/2 which is demonstrated in the following graph.
What happens, though when we add a constant to x rather than multiply by one. We get the equation y = sin (x + C). From the previous case, you might assume that once again the period for this function will change, but how? Take a look at the following graphs when C>0 and C<0.
graph of y = sin x y = sin (x +1) y = sin (x+ 2) y = sin (x -1) y = sin (x - 2)
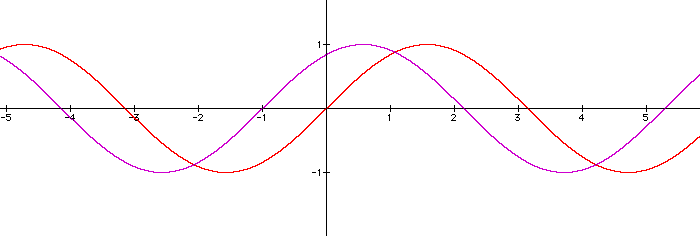
The first thing that I notice is that our graph has been offset horizontally by the value of C.
Let us now add a constant to the value of sin x. I have chosen the following values for D: 1, 2, 3, -1, -2 ,-3.
y=sin x +1; y=sin x +2; y=sin x+3; y=sin x-1; y=sin x -2; y = sin x -3
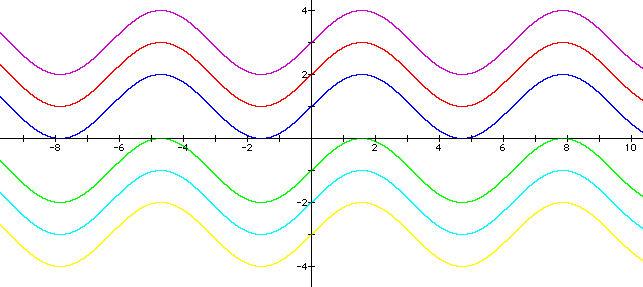
So when we add a constant to the value of sin x, we are offsetting the curve vertically (either positively or negatively depending on the value of D).