An iteration is a process of repeating the same procedure over and over again. A fractal is a geometric figure that is created using iteration. The diagram below shows an example of iterations using GSP.

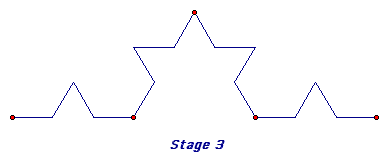
Click HERE to continue the iteration above beginning with stage 3.

Using the above iteration, we can design what is known as the Koch snowflake. This design is constructed by beginning with an equilateral triangle and building equilateral triangles on all sides such as what we did in the previous exercise. The following are stages of the Koch snowflake.

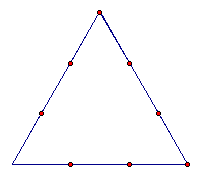
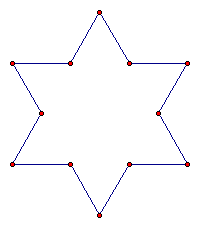
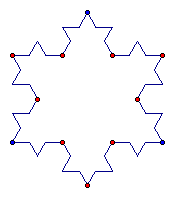
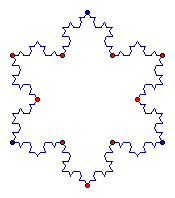
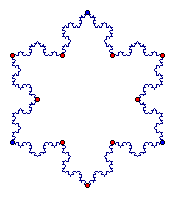
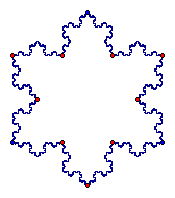
An interesting characteristic of the Koch snowflake deals with the perimeter. If we begin with an equilateral triangle of side 3, then our perimeter is 9. But if we continue building onto the sides of the triangle our perimeter will increase. Each side of the triangle will become 4 segments with a length 1/3 as long. So we could take our side length of 3, multiply it by 4/3 and then by 3 since we have 3 sides. Our second stage will bring the perimeter to 12. Stage three will bring the perimeter to 16.

Each time we iterate, our perimeter will increase. If we think of doing this an infinite number of times, then our perimeter will continue to increase infinitely. But our perimeter is bounded by an area of the cirumscribed circle. So although our perimeter is infinite, our area is finite!

Another example of fractal geometry is the Sierpinski triangle shown below.

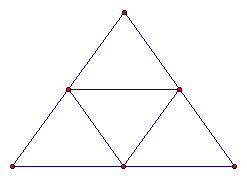
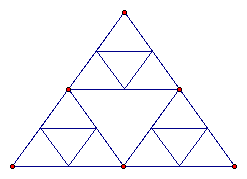
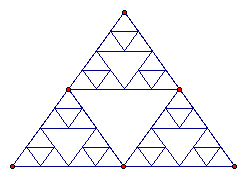
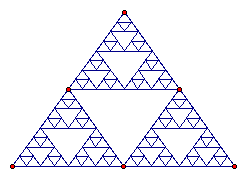
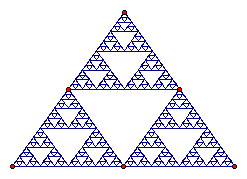
We can see how the process of repeating the same procedure leads to the last figure.

Now, remember Pascal's Triangle! Something interesting occurs when we take Pascal's Triangle and remove all but the odd numbers as shown below.

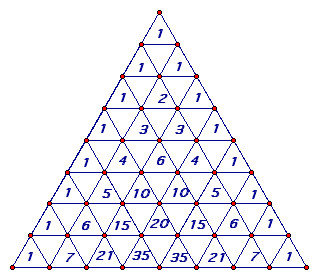
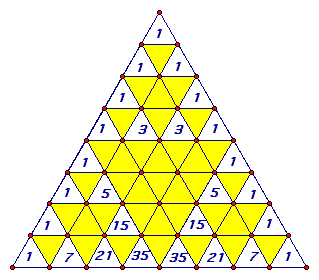
What we have is a Sierpinski Triangle!

Let's look at another famous fractal. This one is called the Jurassic Park Fractal. (This image is used in the chapter headings of the book with an additional iteration completed for each new chapter.) We begin with a line segment, then rotate it 90 degrees. We iterate this process again and again as follows.

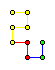
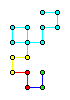
After many iterations, we have the following:

RETURN to Phyllis' home page