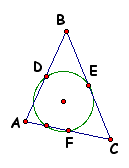
The Nine-Point Circle of a triangle passes through the midpoints of the sides, the feet of the altitudes, and the three midpoints of the segments from the respective vertices to the orthocenter.

We will look at two properties of the nine-point circle.

1. The radius of the nine-point circle is one-half the length of the radius of the circumcircle.

2. The center of the nine-point circle is the midpoint of the segment defined by the orthocenter and the circumcenter.

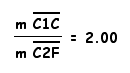
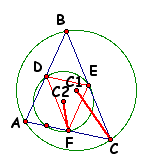
Proof for #1:

Since Triangle DEF is the medial triangle, it is similar to Triangle ABC. Similar triangles have corresponding parts that are proportional (including altitudes, angle bisectors, etc.) and we know that the segment connecting the midpoints of any two sides of a triangle are parallel to and 1/2 the length of the third side. Thereore, the distance from C1 to C is twice the distance from D2 to F.

Proof for #2:

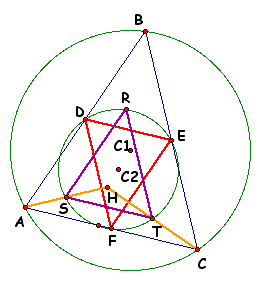
Since S and T are midpoints of semgnets BH and CH, then ST is congruent to DE by the triangle midsegment theorem. Therefore, triangles DEF and TSR are congruent since they share the same circumcenter. Therefore, the triangles are symmetric around the center C2 and their orthocenters will also be symmetric. But since H is the orthocenter of triangle RST and C1 is the orthocenter of triangle DEF, we know that C2 is the midpoint of HC1.

RETURN to Phyllis' home page