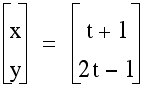
A parametric curve in the plane is a pair of functions where the two continuous functions define ordered pairs (x,y). We call 't' our parameter. In many applications, we think of x and y "varying with time t" or the angle of rotation that some line makes from an initial location.

Let us look at the following parametric equations.

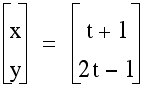
And if we graph this parametric equation for 0 < t < 5 we see the following:

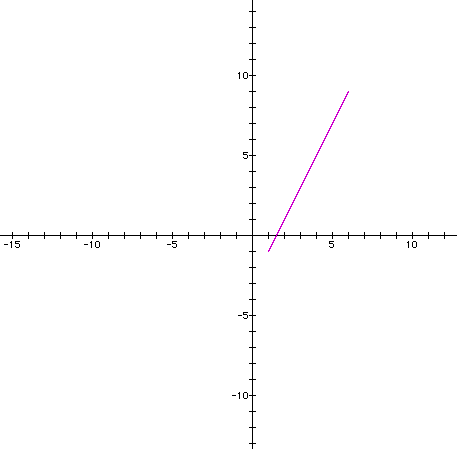
We can conclude from looking at the table and the graph that as the range of 't' becomes larger, then the length of the line will become longer. This can help us understand the concept of parametric equations. In this equation, 0 and 5 are the parameters.

Let us now look at some other parametric curves which involve trigonometric functions. Let us look at x = a cos (t) and y = b sin (t) for different values of 'a' and 'b'.

Our range for 't' in these three equations is 0 < t < 2pi

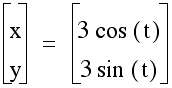shown below in red

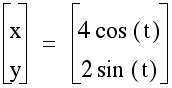shown below in purple

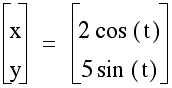shown below in blue

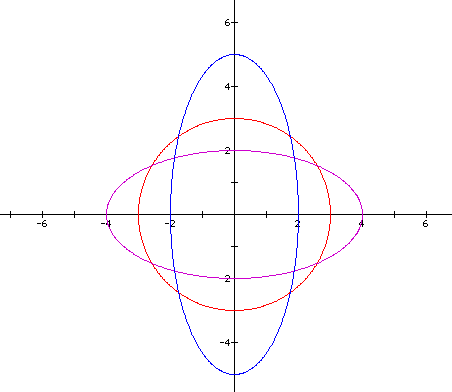
Our graph shows when a and b are the same we have a circle, when a > b we have an ellipse with horizontal elongation and when b < a we have an ellipse with vertical elongation.

Now, look what happens if we let 'a' and 'b' equal 't' in the above functions.

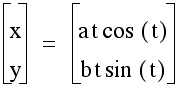for 0 < t < 2pi, and a=1, b=1

The graph of this shows:

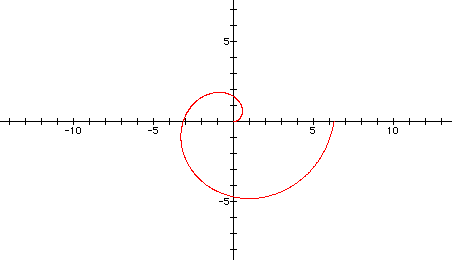
and if we graph the following where 'a' > 'b' and 0 < t < 4pi, we have

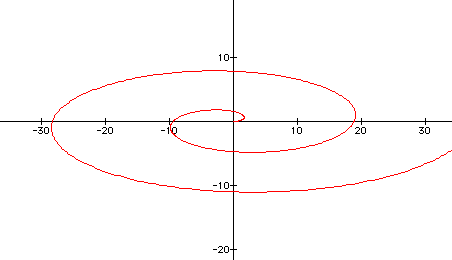
So, we see in all equations how as the parameter 't' is increased the length of the curve increases with respect to 't'.

RETURN to Phyllis' home page