The following is an investigation of the polar equation:

If we let a, b and k equal 1 and graph the function, we have the following:

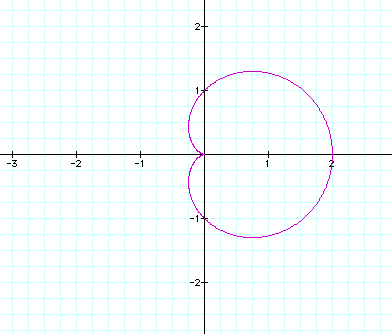
Now, we will let a and b remain as 1 and vary k as an integer to see what the graph produces.

is graphed in purple

is graphed in red

is graphed in blue

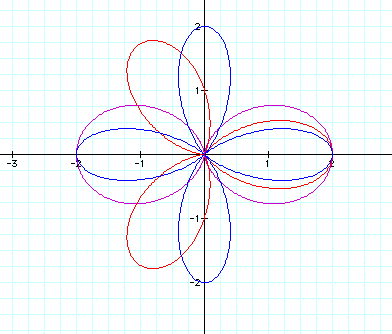
We can begin to see that 'k' possibly produces the number of 'leaves' of the graph. How many leaves will

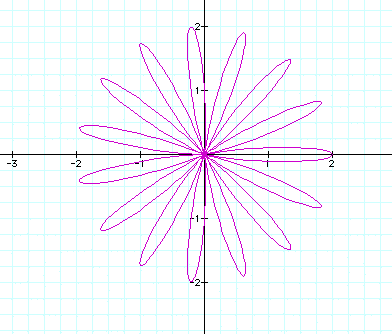
Now we will leave k constant, say 3, and look at a graph of

where a < b. A graph of 1 +2 cos 3is shown below

and

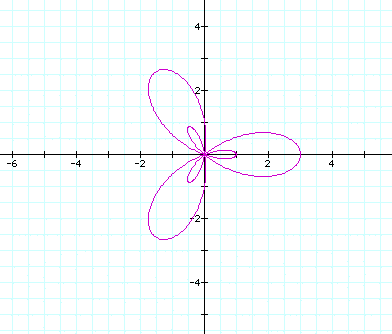
so it appears that if a < b, we have a new inner leaf design, and as b increases the size of the leaves increase.

We will now look at what happens to the graph when b > a. Let us look at

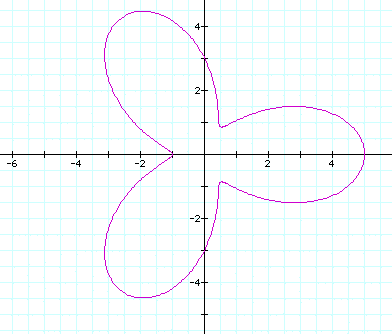
It appears that the leaves are losing their definition. Let's look at

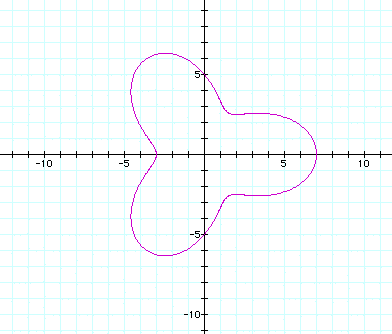
and finally

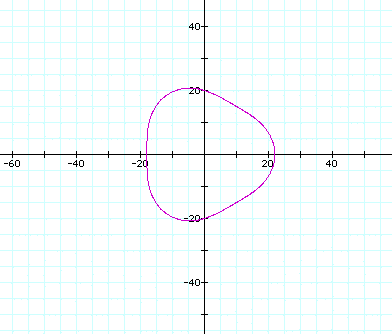
so as a increases we loose our leaf shape completely.