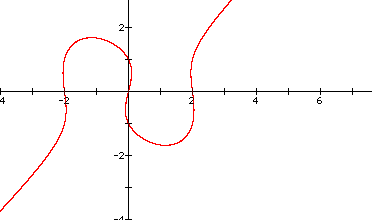
Below is a graph of:
What happens to the graph if the '4' is replaced by other numbers, such as 5, 3, or 1?
x(x^2 - 4) = y(y^2 - 1)
x(x^2 - 5) = y(y^2 - 1)
x(x^2 - 3) = y(y^2 - 1)
x(x^2 - 1) = y(y^2 - 1)
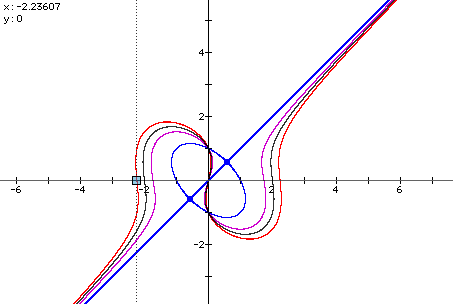
The graph widens as the 4 is replaced by larger numbers and becomes more narrow if the 4 is replaced by smaller numbers. The graph of y(y^2 - 1) = x(x^2 - 1) appears different, however, from the others. This happens when the two constants are the same on both side of the equations. If we replace both the 1's in the equation with 5's, we will the same line y=x, but the circle will be larger. This is because all the values where y and x are equal are solutions to the equation, but there are other points that satisfy the equation such as x = 1, y = -1 and x = -1 and y = 1.
Let's look at the graph with the line 'y = x' added.
All the curves appear to be asymptotic to the line 'y=x' and to each other?
What equation gives the following graph?
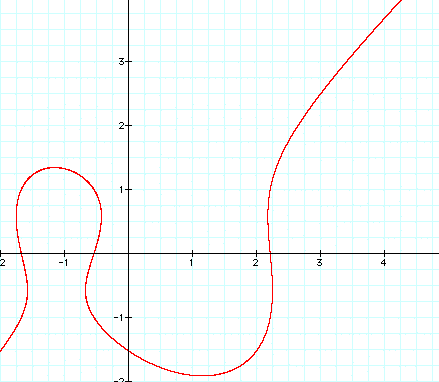
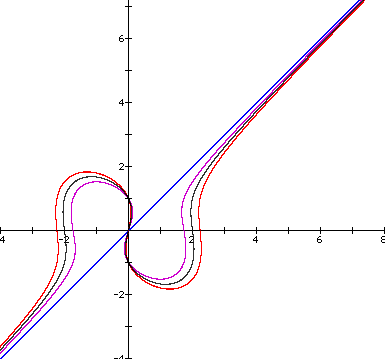
This graph is created by adding '2' to the right side of the equation. Shown below are graphs where we add numbers to the right side of the equation.
x(x^2 - 4) = y(y^2 - 1)
x(x^2 - 4) = y(y^2 - 1) + 2
x(x^2 - 4) = y(y^2 - 1) + 1
x(x^2 - 4) = y(y^2 - 1) - 1
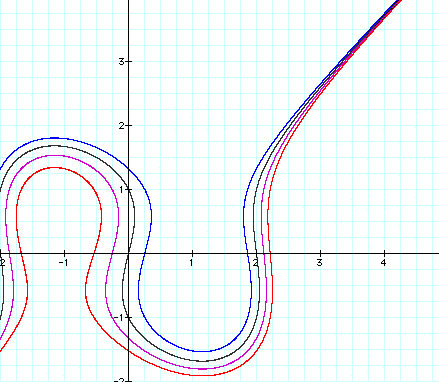
We can see that adding positive numbers causes the curve on the right to widen while causes the curve on the left to become more narrow. Adding negative numbers causes the curve of the graph to widen on the left and become more narrow on the right side.