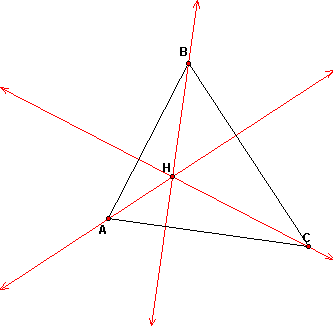
Take any acute triangle and construct the altitudes. The point of concurrency of the altitudes of a triangle is called the orthocenter. We denote this point H.

Let us see what happens when the triangle is obtuse.

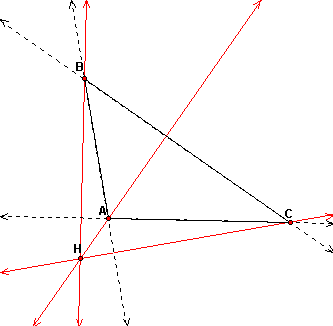
H is now a point outside the triangle. We can see that H does not have to be in the interior of the triangle. Rather, for an obtuse triangle, H lies on the lines extended along the altitudes.

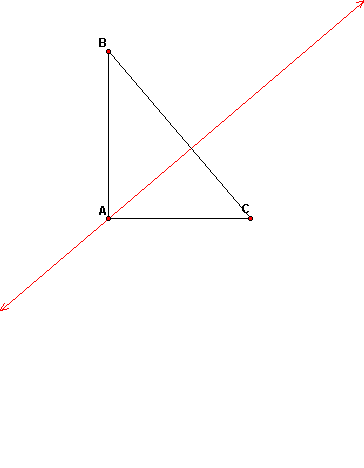
Our third case would involve a right triangle. Can you guess where the orthocenter lies on a right triangle? Think about the altitudes of a right triangle. Where do two of the altitudes lie? Where is H in the diagram below?

In the above diagrams, we have shown that the altitudes of the triangles are concurrent. Let's look at a proof of this using Geometer's Sketchpad.

Construct triangle ABC along with the midpoints of its sides and connect the midpoints of the sides to form triangle DEF.

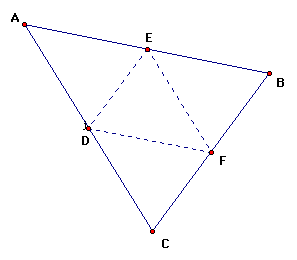
What can be said about the relationship between the perpendicular bisectors of triangle ABC and the altitudes of triangle DEF? Since the segments connecting the midpoints of two sides are parallel to the third side, then the perpendicular passing through E would also be perpendicular to DF. Therefore, the perpendicular bisector of AB is an altitude of triangle DEF. If we can show that the perpendicular bisectors of triangle ABC are concurrent, then the altitudes of triangle DEF are concurrent.

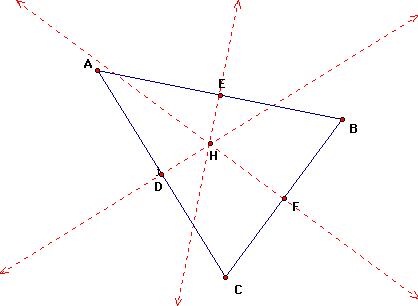
Point H in the above diagram is the same distance from C as it is from B and C because all points on the perpendicular bisector are equidistance from the endpoints of the segment. Therefore in the diagram below segment HA is congurent to segments HB and HC making H equidistance from all three vertices.

RETURN to Phyllis' home page