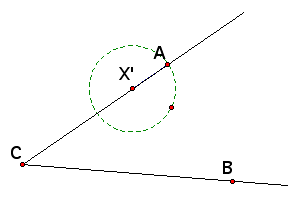
Given three points A, B, and C. Draw a line intersecting AC in the point X and BC in the point Y such that
To begin this construction, select a random point X' on AC. Next construct a point through A with center X' as shown:

Next, construct a circle with radius AX' with center B
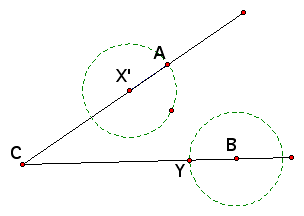
We now have AX' congruent to YB. If we connect points A and B, then construct a line through Y parallel to AB with the intersection of this parallel line marked as point Y', we will have AX' congruent to X'Y' congruent to YB.

all we need to do is to project Y' through the ray AY' until it intersects BC at Y and we will have accomplished our task. AX' congruent to X'Y congruent to YB.
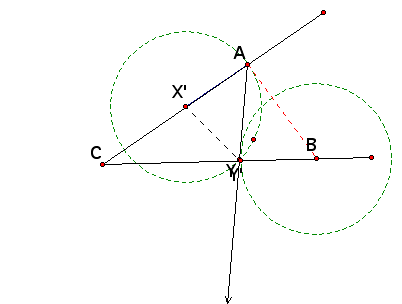
To see a GSP construction of this, click HERE
RETURN to Phyllis' home page.