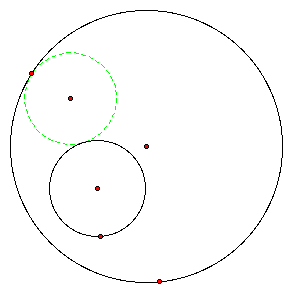
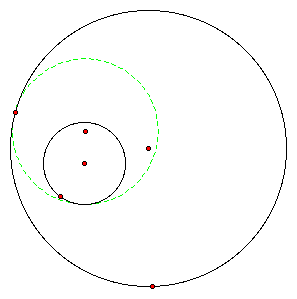
The four figures below show tangent circles constructed to two circles -- a smaller circle inside a larger. To construct these tangent circles click HERE, then use the script tools in GSP.

Diagrams 1 and 2

Diagrams 3 and 4

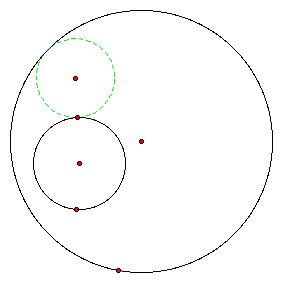
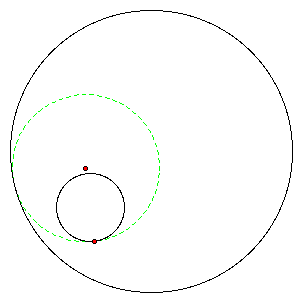
In the diagrams below, a trace of the center of the tangent circles is shown in red.

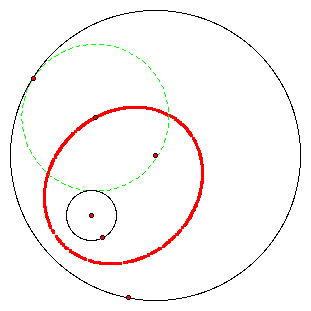
This shows that the locus of the center of all the circles tangent to both circles is an ellipse with foci being the center of the two given circles. The center of the tangent circle was found as shown below.

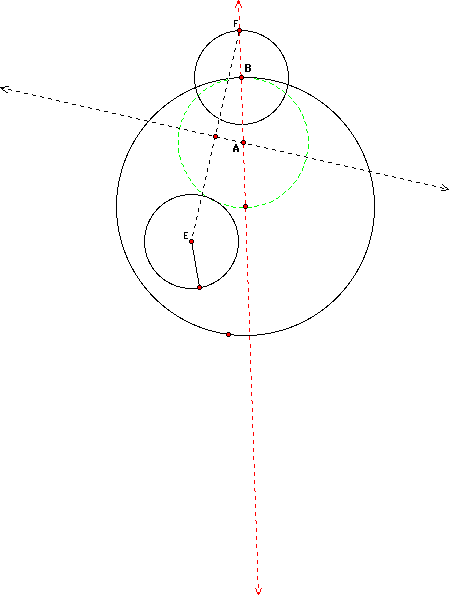
What I found interesting about these tangent circles is that they were all made using the same. When I first begin the constructions, I assumed I would do something totally different according to where the point of tangency I began with was. In diagram #1, I began with the point on the larger circle. In the 2nd diagram I also began with the point on the larger circle, however, the tangent circle was tangent on the outside of the smaller circle. In the third and fourth diagrams, I began with the point on the smaller circle and constructed the two cases as in the first two diagrams.

The last diagram shows how the construction works. In all cases, the center of the tangent circle was located at a point on the diameter that was equidistant from the two circles. How did I find that center? I constructed the perpendicular bisector of segment EF (see last diagram). Where did F come from? Pretty cool, isn't it!!! Try it yourself with GSP.

RETURN to Phyllis' home page