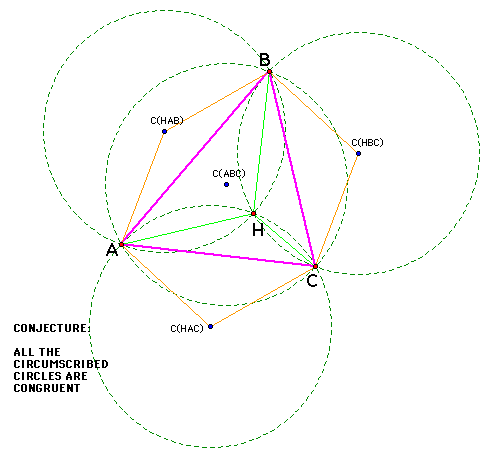
In the figure below, H is the orthocenter of triangle ABC and segments were drawn from H to the vertices of triangle ABC to form triangles HBC, HAB, and HAC. The circumcenters of all four triangles were then constructed and with the circumcenters noted by C(ABC), C(HBC), C(HAB), and C(HAC). In constructing these circumcircles, we can see that they are all congruent, i.e., they have the same radius. The orange segments drawn in are the radii of the circumcircles. Can this be proved?

We will look at how the circumcircles were constructed. Let us look at triangle HBA. We constructed the perpendicular bisectors of each side of this triangle to find the circumcenter which gave us the point C(HAB) equidistant from points A, B and H. But the other circumcircles were constructed the same way. C(HBC) was constructed so that it is the same distance from H and B, and C(HAC) is the same distance from H and A. So if we think about this, we know that our circumcenters are all the same distance from H and a shared vertex from one of the other triangles. This also leads us to the fact that we can also construct a circle with center H that goes through C(HAB), C(HBC), C(HAC) as shown below.

RETURN to Phyllis' home page