Given triangle ABC and Point P anywhere on the plane. If we construct perpendiculars from P to the line which contain the sides of triangle ABC, and locate our three points of intersection (call them RST), then triangle RST is called the pedal triangle for pedal point P.

(To use GSP to construct a pedal triangle click here.)

We can investigate this pedal point and the triangle by looking at several things. For example, what if the pedal point is the circumcenter of triangle ABC? An investigation will show that if we move Point P to the location of the circumcenter, it looks as though the circumcenter for triangle ABC is the orthocenter for triangle RST. This seems logical because of the way the pedal triangle was constructed. If we think about dropping the perpendicular from P to a side of ABC, then moving P to the location of the circumcenter of ABC, our perpendiculars from P will be the same lines as the perpendiculars from the circumcenter which are the perpendicular bisectors of triangle ABC. Have trouble following that? Click here to move P to the circumcenter of triangle ABC.

What if P is the incenter of triangle ABC? Let's do the same thing as above. Move P so that it coincides with the incenter. In doing this we find that incenter of triangle ABC is the circumcenter for triangle RST, our pedal triangle. Consider doing this: Find the incenter of any triangle and construct perpendiculars from the incenter to the sides, then construct a triangle where the perpendiculars intersect the sides. What you will have is an inscribed triangle with a circumcenter that is the same point as the incenter for the larger triangle. Click here to use GSP to investigate this.

Next, let's look at moving P to the orthocenter of triangle ABC. It looks as though P becomes the incenter of triangle RST, the pedal triangle. In other words, the altitudes of triangle ABC become the angle bisectors of triangle RST. This is not so obvious as the above. Can we prove this? In the diagram below, the pedal point P is the orthocenter for triangle ABC.

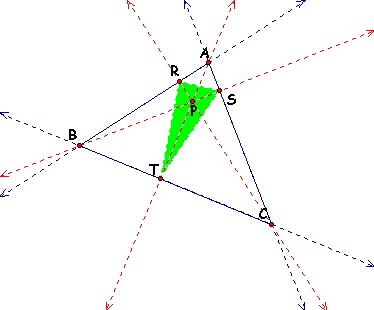
We know that angle PSC and angle PTC are right angles. Therefore, quad PSCT is a quadrilateral that can be inscribed in a circle with diameter PC.

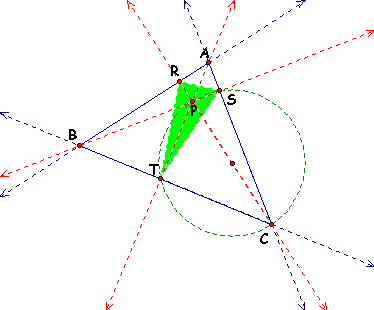
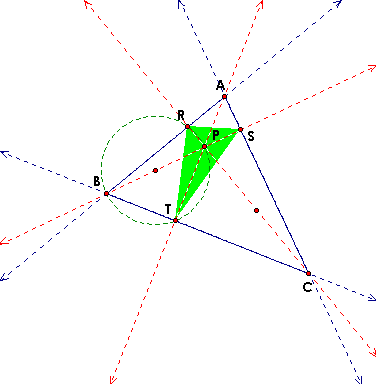
Thus, we know that angle SPC is congruent to angle STC because they are inscribed angles that both intercept the same arc. We also know that angle SPC is congruent to angle RPB because they are vertical angles. Similarly, if we also circumscribe quadrilateral RPTB we will find that angle RTB is congruent to angle RPB. Therefore, angle STC and angle RTB are congruent. Since angles PTC and PTB are right angles, we can subtract and thus we have that angles RTP and STP are congruent.