FINAL ASSIGNMENT
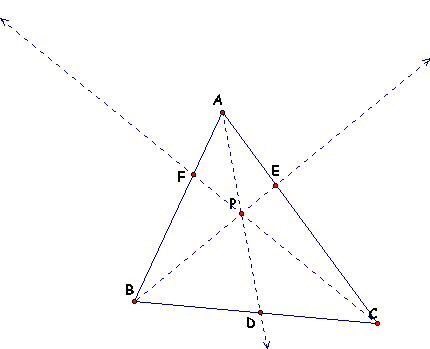
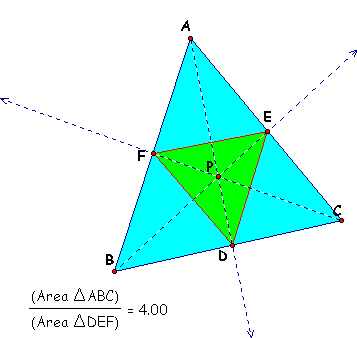
Given any triangle ABC with Point P in the interior. Construct ray AP, ray CP and ray BP. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various locations of P.

If we compute, using GSP, (AF)(BD)(EC) and (FB)(DC)(EA), we get the following:
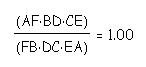
We need to use parallel lines in order to find similar triangles to prove this ratio. If we construct a line through one of the vertices parallel to the opposite side we have the following:
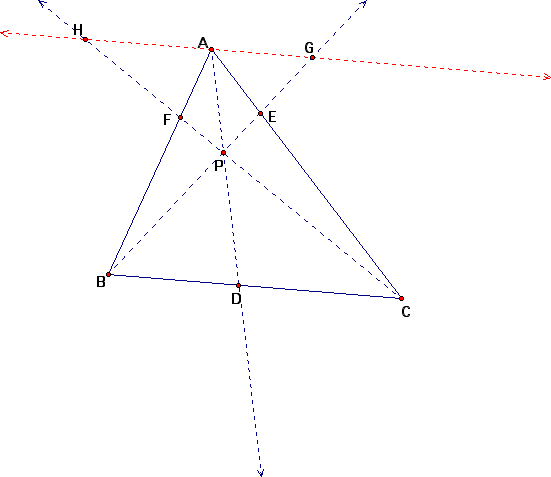
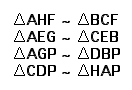
From this we can note that
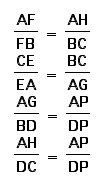
From the last two ratios, we can conclude that
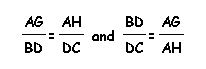
so by multiplying we have
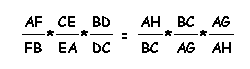
and by cancellation we have
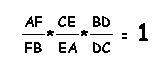
Can this result be generalized so that Point P can be outside the triangle? Click here to use GSP to move Point P outside the triangle. We can see that the ratio remains equal to 1.
We can also look at the area of the triangle DEF and its relationship to triangle ABC. When P is the incenter of triangle ABC, then D, E, and F are all midpoints of the sides and all four smaller triangles formed in the diagram below are congruent. This means that triangle ABC is equilateral and the ratio of the area of triangle ABC to triangle DEF will be 4 to 1. Also, we know that area of ABC = 1/2bh, so the area of DEF = 1/2(1/2b)(1/2h), the ratio is then
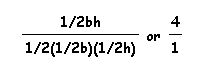
We can conclude that the ratio of triangle ABC and triangle DEF will always be greater than or equal to 4 because the area of triangle DEF is at its maximum when it is equilateral. As P is moved within triangle ABC, either the height or the base will be less then 1/2 of the base or height of the larger triangle. Click here to move Point P within the triangle.
RETURN to Phyllis' home page