I investigate
In my investigation, I set a=b=1 and k takes various values. This is an American textbook version of the "n-leaf rose" problem. It is common knowledge that for the rose curves, we obtain n petals if n is odd and 2n petals if n is even. n takes values greater or equals to 2. The length of each pedal is b. It is useful to examine the rectanglar graph (r verses angle) when we deal with polar equations. The loops of this curve lie between values of for which r = 0 ie.
One of the loops lie between
and 
As the values of k increases, we have more and more loops.
Next, I replace cos() with sin(). We follow the above reasoning to find the intervals where the loops lie which is:
As the values of k increases, we have more and more loops.
The number of loops for
and
are the same.
Next, I investigate the expression for ,
The values of a and b will determine the lenth of each pedal. Suppose a = b =1, i.e the length of each rose pedal is 2. In the interval, [0,2P], r equals to zero when
We compare the values of theta for
and 
when a = b = 1. From the above, we see clearly that will
generate twice as many pedals as compared to ..
For the diagrams below, when k =n (even),
produces n purple pedals each of
length 2.
produces 2n blue pedals each of
length 1.
produces 2n yellow pedals each
of length 1.
Next, I investigated the following 3 polar equations for various k values.
I broke up my investigation into even and odd values of k. For the rest of this webpage, I will put up some observable patterns for the 3 equations as I vary the values of k.
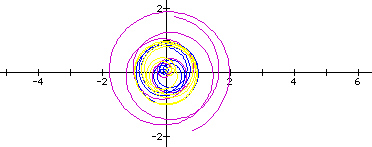
For k=20,
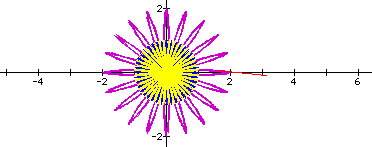
k= 70,
k=100
k=260
k=280
If we take k = multiples of 280, we will observe similar pattern.
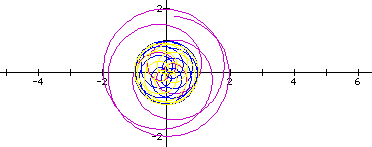
k=320
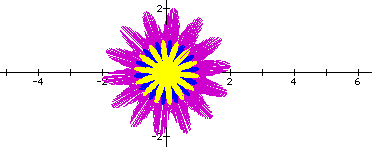
For the diagrams below, k is odd
produces k purple pedals each of
length 2.
produces k blue pedals each of
length 1.
produces k yellow pedals each of
length 1.
k=5
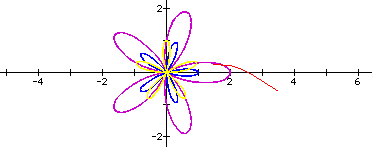
k=71
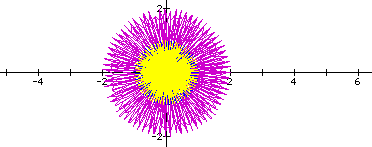
k=191
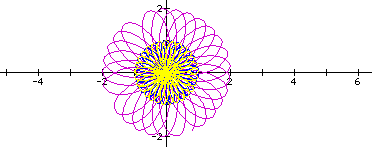
k=263
k=325
k=841
