Construct graphs for the parabola

for different values of a, b and c. (a , b and c can be any rational numbers)

I begin with the simplest type of quadratic function,

This gives me a parabola with vertex (0,0). if a > 0, the vertex is the point with the minimum y-value on the graph. If a < 0, the vertex is the point with the maximum y-value on the graph. We note that y=-ax is a mirror image of y=ax about thr x-axis for the same values of a.

Sketching of Quadratic Functions

Let us compare the following graphs:

We notice that with greater values of a, the graph shrinks by a factor a, creating a narrower parabola.

If a < 0 , the parabola opens more widely with smaller values of a. Hence, we conclude that the coefficient of a determines how widely the parabola

opens.

Investigating c

Next, I investigate how the various values of c affect the shape of

where c can take any rational numbers. From my observations, the point where the parabolas cut the y-axis will be (0,c). the point (0,c) is not the vertex of the parabola. Let a =1 and b = 1. We then have,

We construct this parabola using c =-6,-4,-2,0,2,4,6.

We obeserve that the parabola

cuts the y-axis at (0,c).

The parabola

,

cuts the y-axis at (0,-c). This point is however not the vertex.

Investigating b

I investigated the movement of the parabola of the general form .

I discovered that the movement of the parabola traced another parabola of the form

Next, I investigate what happens when 2 parabolas of the form overlay/intercept. I set a = 1 or -1 and c = -5, 5.

Summary of Results

Case 1

The 2 graphs intercept at 2 points. One of the points is (0,5) for all values of n. When x=0, the 2 graphs has one point of intersection at (0,5). The area of intersection is greater for greater values of n. The graphs move together for the same values of n. When n> 0, graphs move along the positive x-axis. When n<0, the graph moves along the negative x-axis. the following pairs of parabolas produce the same kind of interceptions.

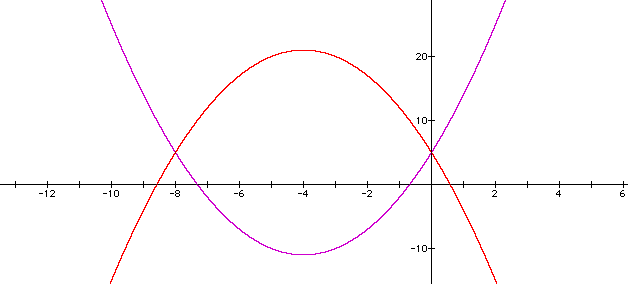
Case 2

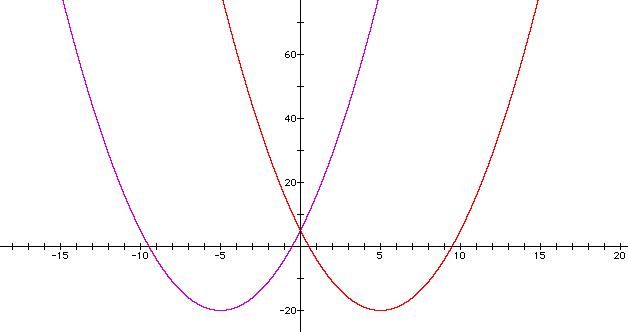
The 2 parabolas intercept at at only 1 point (0,5) for all values of n and they are symmetrical about the point (0,5). They move in opposite directions for the same values of n. The pairs of parabolas that produce similiar interception patterns are

Case 3

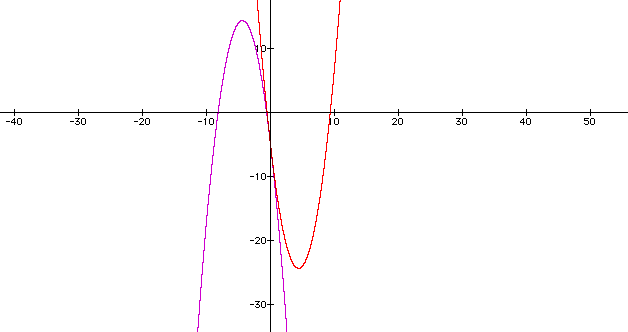
Most of the pairs of parabolas intercept in the above manner.

Case 4

The 2 parabolas never neet and they move together.

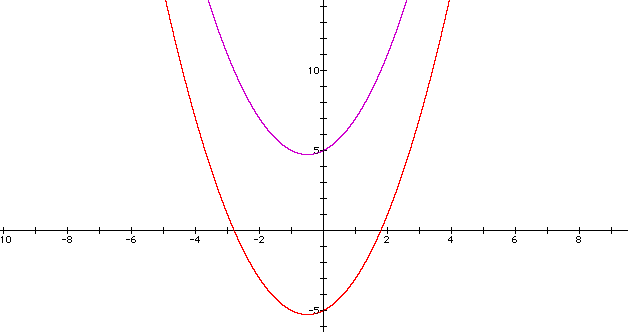
Other pairs of parabola that intercept in the same manner is

If we put a is negative, the above set of parabolas still move together but with the cup facing downwards.

Vertex of Parabola

The vertex of a parabola of the form

is obtained when

Then,

Roots of Parabola

The solutions of a quadratic equation in the general for are given by

Discriminant Rule

To find the total number of roots, we follow the following rules:

If the discriminant is

(1) Positive

The quadratic equation has 2 distict real solutions and its graph has 2 x-intercepts

(2) Zero

The quadratic equation has one repeated real solution and its graph has 1 x-intercpet

(3) Negative

The quadratic equation has no real solution and its graph has no x-intercpets. Its square root is imaginary and yields 2 complex solutions

Test out the discriminant rule in assignment 3 to find out the behaviour of the roots.

Return