

MEDIAN
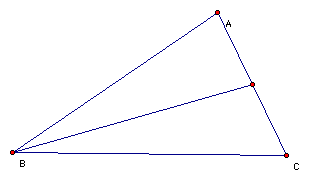
A median of a triangle is a segment from a vertex to the midpoint of the opposite side. The 3 medians of triangle ABC are shown above. The median divides the triangles into 2 equal parts since the 2 triangles share the same altitude and base.
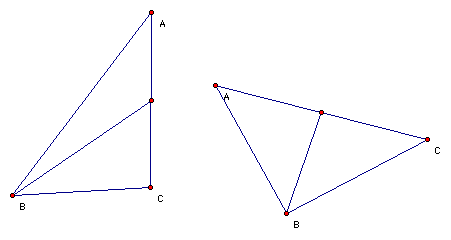
When we construct 2 medians of a triangle together, they interesect at a point G. The third median passes through the same point G, called the centroid, and traingle ABC is now equally divided into 6 parts.
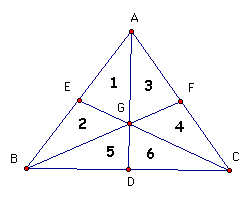
Proof that triangle ABC is now equally divided into 6 parts:
The following pairs of triangles share the same base and altitudes hence they have the same area:
Triangle 1 and 2
Traingle 3 & 4
Triangle 5 and 6
Triangle ABD and ACD
Triangle CED and CEA
Triangle BAF and BCF
Sum of regions (1 + 2 + 5 ) = Sum of regions (3 + 4 + 6) and area of region 5 = area of region 6,
implies
Sum of area of regions (1 + 2 ) = Sum of area of regions (3 + 4)
That is,
2 Area of region 1 = 2 Area of region 3 , hence, area of region1 = area of region 3
2 Area of region 2 = 2 Area of region 4, hence, area of region 2 = area of region 4
2 Area of region 1 = 2 Area of region 4, hence, area of region 1 = area of region 4
2 Area of region 2 = 2 Area of region 3, hence, area of region 2 = area of region 3
Sum of regions (2 + 5 + 6 ) = Sum of regions (1 + 3 + 4)
Since, area of region2 = area of region 1 and area of region3 = area of region 4,
Area of region 5 = Area of region 3
Area of region 5 = Area of region 4
Area of region 6= Area of region 3
Area of region 6= Area of region 4
Sum of regions (4 + 5 + 6 ) = Sum of regions (1 + 2 + 3)
using the same reasoning as above, we have area of region 5 = area of region 2
Hence
Area of region 1 = 3 = 4 = 6 = 5 = 2 = 1.
ORTHOCENTER
When we change the dimensions of the traingle, the centroid always remain in the triangle. Next, we construct the orthocenter (H) of a triangle. The orthocenter of a triangle is the common intersection of the 3 lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side and H lies on the lines extended along the altitudes. When we shift or change the position of A, B or C respectively, G remains in the triangle but H does not.
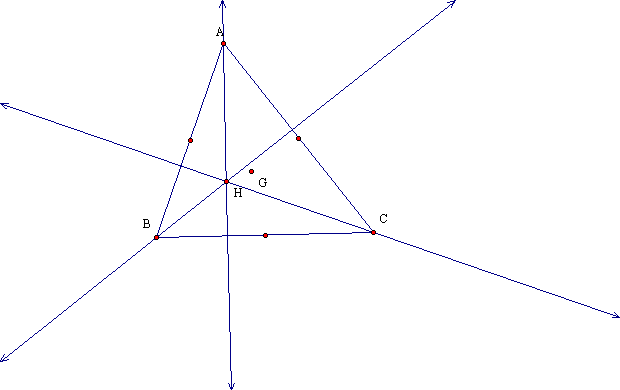
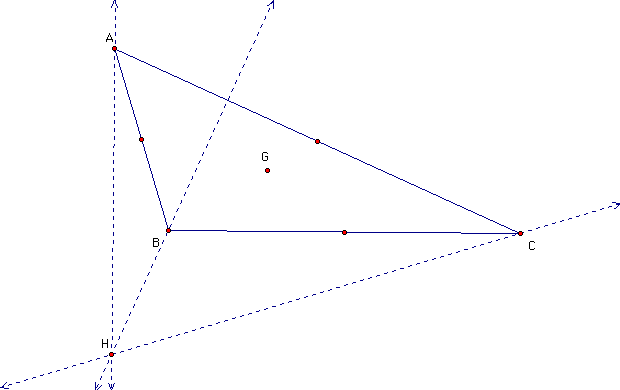
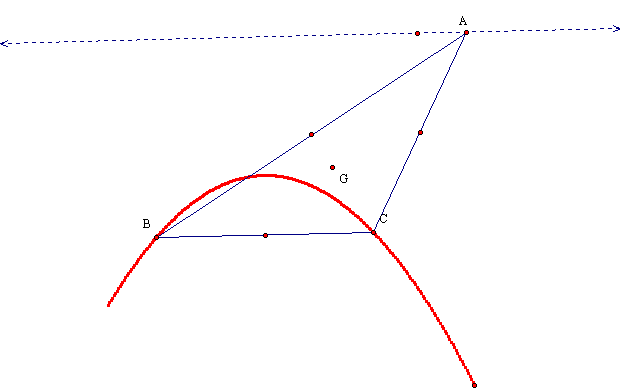
I investigated the movment of H. I constructed a line DE parallel to BC and trace the movement of H when A moves along DE. H seems to form a parabola with directrix DE. Next, I attempted to locate the exact position of H.
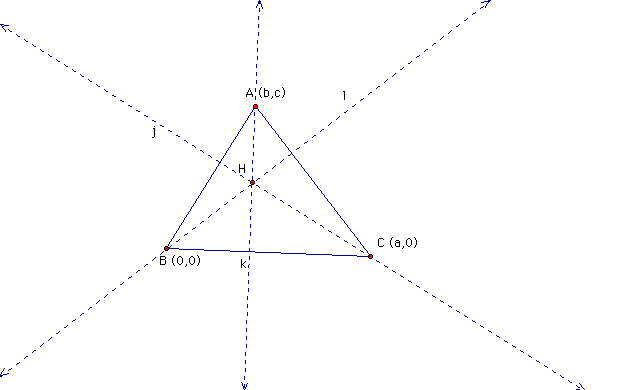
H is the intersection of line k and l. The equation for line AC is easy to find using the points A(b,c) and C(a,0).
Gradient of AC is
Gradient of line l is
Equation of line l
Equation of line k is given by x =b
Hence, H takes up the following values:
It simply means, for any given triangle, the x-coordinate of H follows the x-coordinate of one of the vertex of the triangle. The general expression for the y-coordinate of H suggests that y takes any inside and outside the triangle. The equation of the parabola is
Ckeck:
When x=a,
To locate the vertex:
The vertex is at
and
CIRCUMCENTER (C)
The circumcenter C is a point where the perpendicular bisectors of each side of the triangle meet. from our construction, we note that C may be outside the triangle.
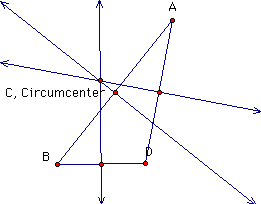
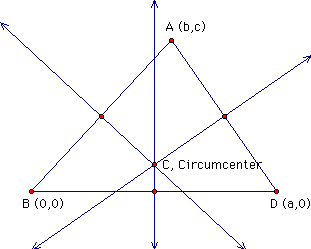
We want to show that the 3 bisectors of the sides are concurrent.
Equation of segment AB
Midpoint of AB is
The perpendicular bisector of AB has a gradient of ![]() and it passes through the midpoint of AB. Hence,
and it passes through the midpoint of AB. Hence,
where d is the y-intercept. Then,
We do the same to find the equation for the perpendicular bisector of AD. We get
Similarily, the perpendicular bisector of BD is
The 3 lines intercept at
The 3 bisectors are thus concurrent.
Incenter
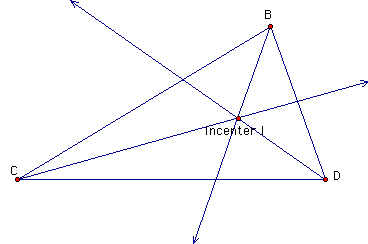
The three angle bisectors of the internal angles of a triangle are concurrent.
Nine-Point Circle
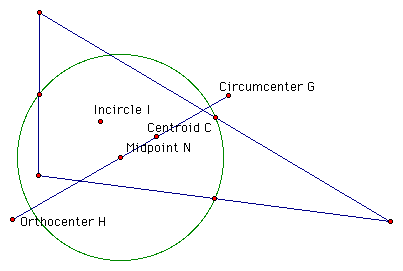
We want to prove that H, G and C are collinear and HG = 2GC.
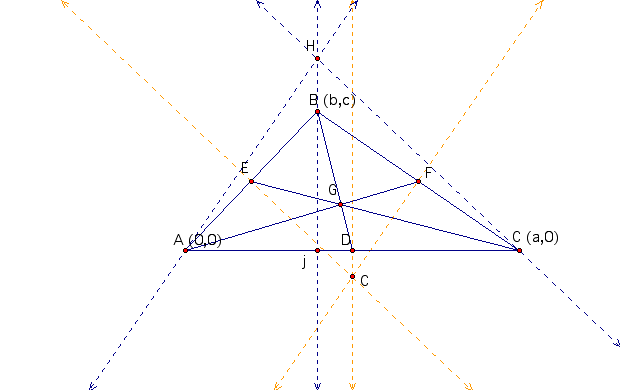
Coordinates of C:
Coordinates of H:
Coordinates of G:
Consider 2 points C and H:
Gradient of segment CH is
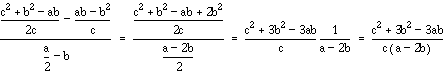
y-intercept of segment CH is given by
Equation of CH is
It can be shown easily that Point G lies on the above line. Hence, HGC are collinear.
Medial Traingle
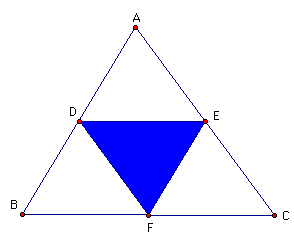
If we take any triangle, construct a triangle connecting the 3 midpoints of the sides, we obtain the medial triangle. It is similiar to the original triangle and one quarter its area.
Proof
Area of Triangle ABC is
Area of Triangle DEF is
This can be proved using paper folding exercise.
Interior Triangle
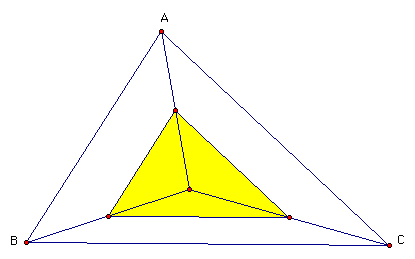
The shaded triangle is
(a) similar to triangle ABC
(b) congruent to the medial triangle