

Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area?
I construct a triangle and its median. Using two of the medians, I construct a second triangle with the three sides sharing the same lengths of the 3 medians from the original triangle DLI.
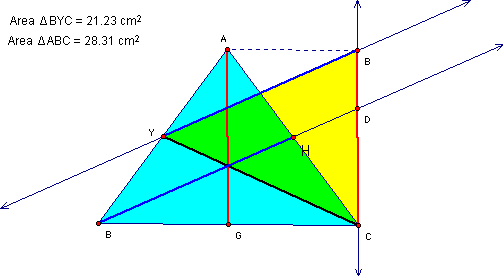
The two triangles do not have the same area and they are not congruent.
Parabola
We know that a parabola is the set of points equidistant from a line, called the directrix, and a fixed point, called the focus. We assume that the focus is not on the line. I construct a parabola using a fixed point for the focus and a line (segment) for the directrix.
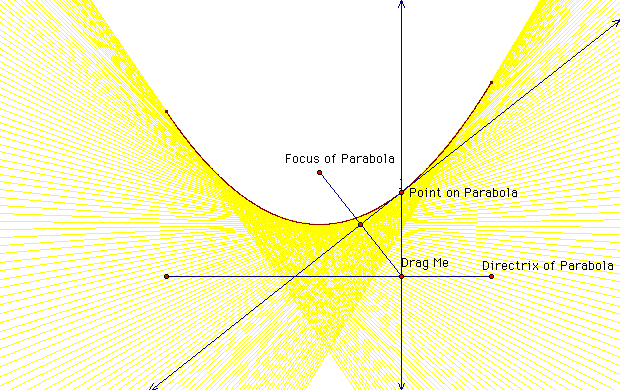
Brief description of GSP Construction
Draw a line. Call this line the directrix. Create a point above the directrix and call it the focus. Create another point, D on the directrix. Connect Focus and D. Find the midpoint and construct the perpendicular bisector through the midpoint. Construct a perpendicular line through D. The intersection between the 2 perpendicular lines is the point P on the parabola. connect FD and FA respectively. The above construction works due to the the properties of a perpendicular bisector.
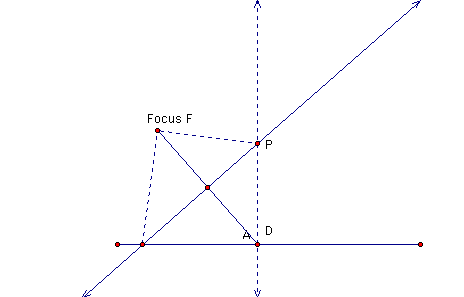
The points lying on the perpendicular AP is equidistant from AF to AD and FP to PD. Hence, the 2 triangles PFA and PDA are congruent. Hence, P is the set of points equidistant from the directrix and the focus.
Ellipse & Hyperbola
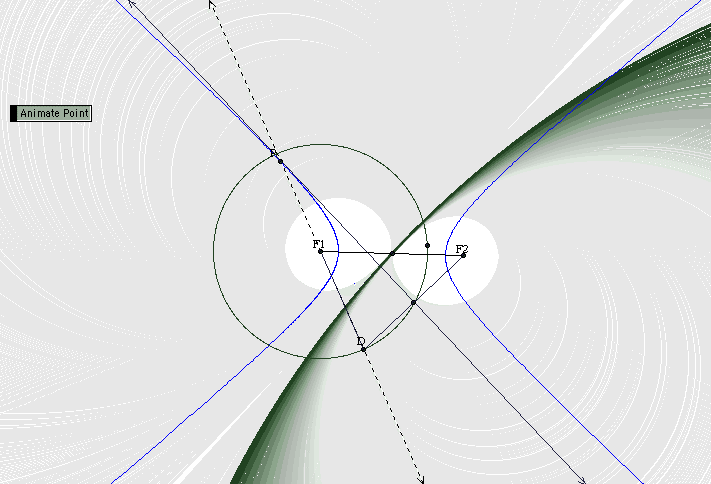
The construction is basically the same as above. Suppose now the directrix is a circle. Let F2 be any point in the plane other than the center of the circle. Assume that F2 is not on the circle but it can be either inside or outside the circle. Then, an ellipse is generated when F2 is inside the circle. A hyperbola is generated when F2 is outside the circle.
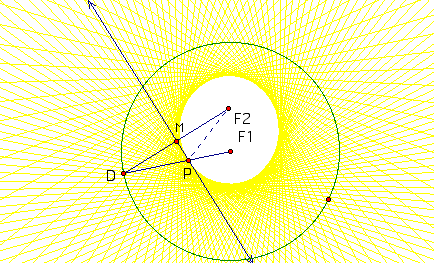
When F2 is inside the circle, we see from the construction above that triangle DMP is congruent to triangle F2MP. This is due to the property of the perpendicular bisector where F2P = DP. Then, DF2 +PF1 =radius of the circle = constant. That is, distance from P to F1 + Distance from P to F2 = radius of circle = constant. We obtain an ellipse.
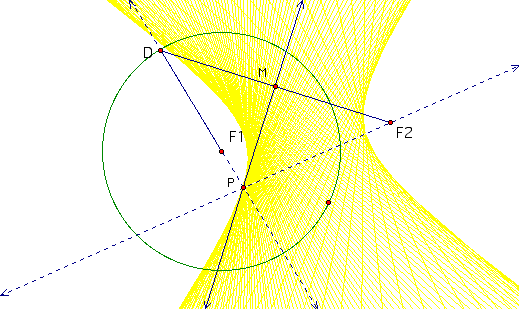
When F2 is outside the circle, we see from the construction above that triangle DMP is congruent to triangle F2MP. This is due to the property of the perpendicular bisector where F2P = DP.
Then, DP-PF1 =radius of the circle = constant. We thus obtain a hyperbola.
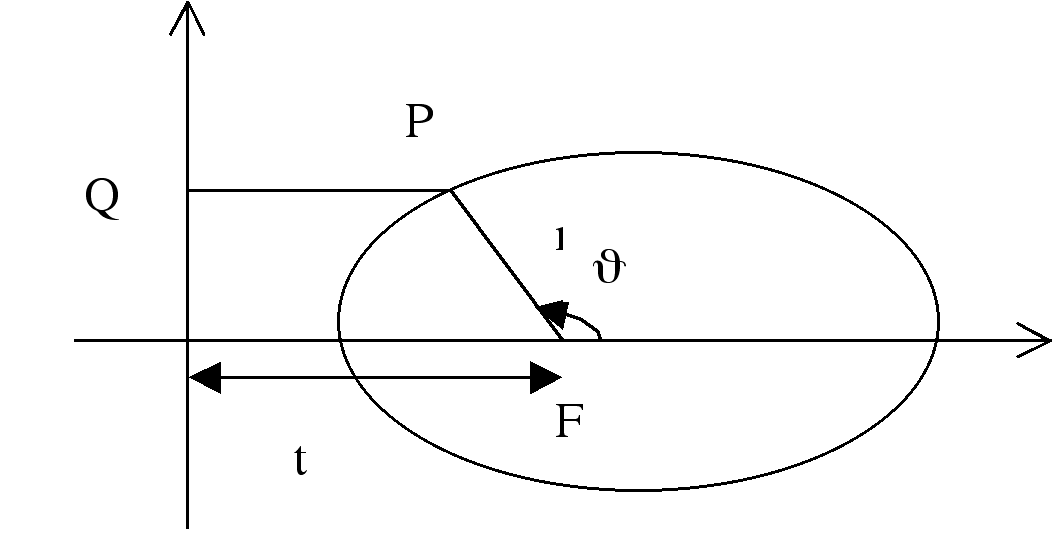
I would like to discuss the straight line directrix of the ellipse. We put an ellipse with one of its focus at the origin.
A standard equation to describe an ellipse is given by
where![]()
and a and b is the length of the semimajor and semi minor axis respectively. I would like to show that eccentricity e of the ellipse is given by c=ea.
From the above diagram,
squaring both sides, re-arranging and simplfying the terms would give us
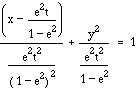 .........(2)
.........(2)We compare (1) and (2)
we have,
Hence, c=ea
I would like to now discuss the circle directrix of the ellipse and see if there is any relationship between the straight line and circle directrix for the ellipse.
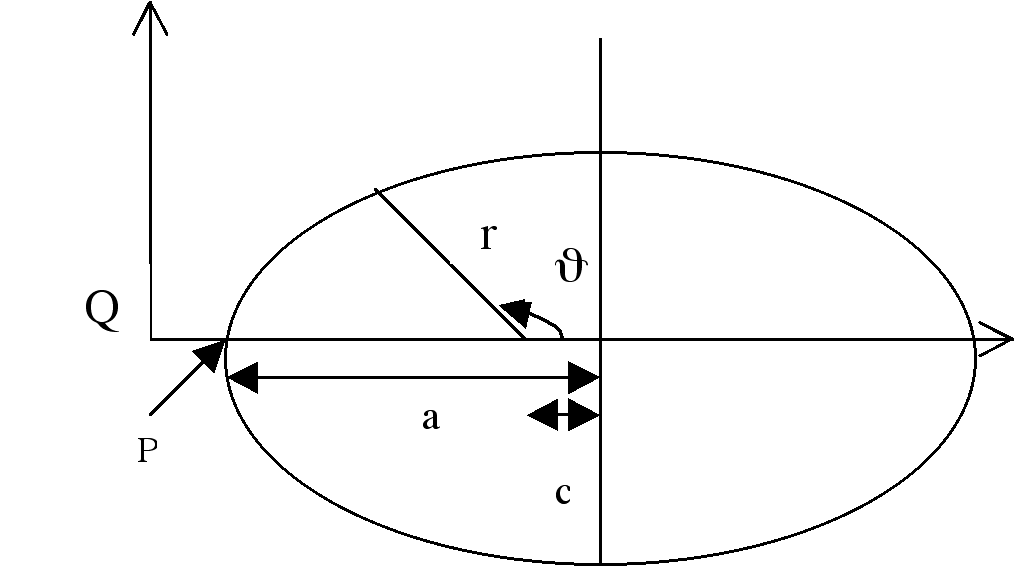
One of the foci, F, of the ellipse is at the origin.
If the circcle and straight line directrix are tangent to one another,
Solving for c,
we find that
This is the eccentricity when the two directrix meet.
Next, I constructed the lemniscate from the hypebola that I constructed above. I took the midpoint ,M , of the segment formed by the two foci of the hyperbola and then made a variable point Q on the hyperbola and set it as the center of a circle that passes through the midpoint M. I trace the envelop of circles generated as Q moves on the hyperbola. This envelop is the lemniscate and is the inversion of the hyperbola in circle.
I place the fixed point nearer to one of the foci of the hyperbola (not the midpoint of the segment connecting the 2 foci). The lemniscate is slightly different from above. The shape of one of the lemniscate(s) is bigger on the side where distance from the fixed point to the focus is larger.

When I place the fixed point of the envelop at one of the foci, I obtain an envelop that defines a circle.

For the ellipse, I took a variable point on the ellipse and a fixed point outside the ellipse. I set the variable point as the center of the circle and it passes through the fixed point. When this variable point moves round the ellipse, I obtain the trace of an envelop of circles.
